
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据条件可以得出$-\frac{m}{3}\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$,并设$-\frac{m}{3}\overrightarrow{OC}=\overrightarrow{OM}$,这样即可得出A,B,M三点共线,画出图形,并得到$\frac{{S}_{△AOB}}{{S}_{△ABC}}=\frac{m}{3+m}=\frac{4}{7}$,从而解出m的值.
解答 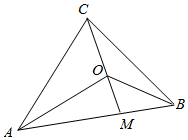 解:如图,令$-\frac{m}{3}\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}=\overrightarrow{OM}$,则:
解:如图,令$-\frac{m}{3}\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}=\overrightarrow{OM}$,则:
A,B,M三点共线;
$\overrightarrow{OC}$与$\overrightarrow{OM}$共线反向,$\frac{|\overrightarrow{OM}|}{|\overrightarrow{CM}|}=\frac{m}{3+m}$;
∴$\frac{{S}_{△AOB}}{{S}_{△ABC}}=\frac{|\overrightarrow{OM}|}{|\overrightarrow{CM}|}=\frac{m}{3+m}=\frac{4}{7}$;
解得m=4.
故选C.
点评 本题考查向量的数乘运算,A,B,C三点共线的充要条件:$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,且x+y=1,共线向量基本定理,三角形的面积公式.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
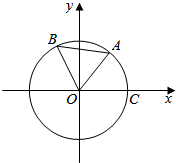 如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,角∠AOB=$\frac{π}{4}$,若点A的坐标为($\frac{\sqrt{2}}{10}$,$\frac{7\sqrt{2}}{10}$),记∠COA=α.
如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,角∠AOB=$\frac{π}{4}$,若点A的坐标为($\frac{\sqrt{2}}{10}$,$\frac{7\sqrt{2}}{10}$),记∠COA=α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-7=0 | B. | x+2y-5=0 | C. | x-2y-1=0 | D. | 2x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,A1在底面ABC的投影是线段BC的中点O.
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,A1在底面ABC的投影是线段BC的中点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com