【题目】过点A(3，－1)且在两坐标轴上截距的绝对值相等的直线有____条，方程为：_____
【答案】 3 
、
、
【解析】
本题分三种情况讨论：①截距不为0，且截距相等，设出截距，利用截距式表示直线方程，将点P代入直线方程，即可求出参数值，将参数值待入直线方程再化简，即可求出方程；
②截距不为0，且截距互为相反数，设出截距，利用截距式表示直线方程，将点P代入直线方程，即可求出参数值，将参数值待入直线方程再化简，即可求出方程；
③当截距为0时，设相应的直线方程，代入点P坐标，求解即可.
①当截距不为0，且截距相等时，设直线的截距为a，则直线方程为：
，将点P坐标代入直线方程，解得：
，所以直线方程为：
；
②当截距不为0，且截距互为相反数时，设直线的横截距为a，则纵截距为-a，则直线方程为：
，将点P坐标代入直线方程，解得：
，所以直线方程为：
；
③当截距为0时，设直线方程为：
，代入点P，可得：
，
直线方程为：，故直线有3条.
科目：高中数学 来源： 题型：
【题目】己知n为正整数，数列{an}满足an＞0，4（n+1）an2﹣nan+12=0，设数列{bn}满足bn= 
（1）求证：数列{ 
}为等比数列；
（2）若数列{bn}是等差数列，求实数t的值：
（3）若数列{bn}是等差数列，前n项和为Sn ， 对任意的n∈N* ， 均存在m∈N* ， 使得8a12Sn﹣a14n2=16bm成立，求满足条件的所有整数a1的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
:
的离心率
，过椭圆的上顶点
和右顶点
的直线与原点
的距离为
，
（1）求椭圆的方程；
（2）是否存在直线
经过椭圆左焦点与椭圆交于
,
两点，使得以线段
为直径的圆恰好经过坐标原点？若存在,求出直线方程；若不存在,请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中，将底面是直角三角形，且侧棱与底面垂直的三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示（网格纸上正方形的边长为1），则该“堑堵”的表面积为（ ）
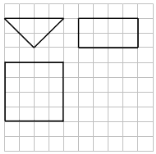
A. 8 B. 16+8
C. 16+16 D. 24+16
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面是边长为2的菱形，且∠BAD= 
，AA1⊥平面ABCD，AA1=1，设E为CD中点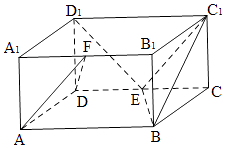 
（1）求证：D1E⊥平面BEC1
（2）点F在线段A1B1上，且AF∥平面BEC1 ， 求平面ADF和平面BEC1所成锐角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校1800名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50名学生组成一个样本，将测试结果按如下方式分成五组：第一组
，第二组
……，第五组
，如图是按上述分组方法得到的频率分布直方图.
（1）请估计学校1800名学生中，成绩属于第四组的人数；
（2）若成绩小于15秒认为良好，求该样本中在这次百米测试中成绩良好的人数；
（3）请根据频率分布直方图，求样本数据的众数、平均数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，函数
.
（Ⅰ）当
时，解不等式
；
（Ⅱ）若关于
的方程
的解集中恰有一个元素，求
的取值范围；
（Ⅲ）设
，若对任意
，函数
在区间
上的最大值与最小值的和不大于
，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
