
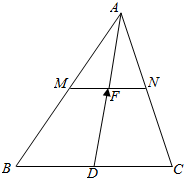
 在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.
在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标. 分析 利用向量的坐标运算、平行四边形的法则即可得出.
解答 解:A(7,8),B(3,5),C(4,3),
∴$\overrightarrow{AB}$=(-4,-3),$\overrightarrow{AC}$=(-3,-5).
∵M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,
∴F是AD的中点,
∴$\overrightarrow{DF}$=-$\frac{1}{2}$$\overrightarrow{AD}$=-$\frac{1}{2}$×$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=($\frac{7}{4}$,2).
点评 本题考查了向量的坐标运算、平行四边形的法则,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
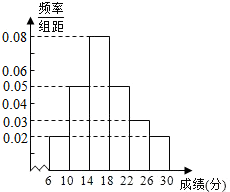 某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com