
分析 (1)由f(1)=-2得a,b的方程①,由f(x)≥-2x即恒成立x2+xlga+lgb≥0对x∈R恒成立,得△=lg2a-4lgb≤0,消掉a得b的不等式,由此可得关于b的方程,从而得到b值,进而得到a值,进而得到所求解析式;
(2)运用分段函数的形式求得g(x),对m讨论,分当m-1≥3,当1<m-1<3,当m-1≤1,讨论单调性即可得到最小值h(m);
(3)讨论m的范围,解不等式,先求交集,再求并集即可得到所求不等式的解集.
解答 解:(1)由f(1)=-2,得f(1)=1-(lga+2)+lgb=-2,化简得:lga-lgb=1,
∴$\frac{a}{b}$=10,即a=10b.
又由x∈R,f(x)≥-2x恒成立.知:x2-(lga+2)x+lgb≥-2x,即x2-xlga+lgb≥0对x∈R恒成立,
由△=lg2a-4lgb≤0,得(1+lgb)2-4lgb≤0,
即(lgb-1)2≤0,只有lgb=1,不等式成立,即b=10,∴a=100,
即有f(x)=x2-4x+1;
(2)g(x)=x2-4x+1+2|x-m+1|=$\left\{\begin{array}{l}{(x-1)^{2}+2-2m,x≥m-1}\\{(x-3)^{2}-10+2m,x<m-1}\end{array}\right.$,
当m-1≥3,即m≥4时,即有g(x)在(-∞,3)递减,在(3,m-1)递增,在(m-1,+∞)递增,
即有x=3处取得最小值,且为2m-10;
当1<m-1<3即为2<m<4,即有g(x)在(-∞,m-1)递减,在(m-1,+∞)递增,
则x=m-1处取得最小值,且为m2-6m+6;
当m-1≤1即m≤2,即有g(x)在(-∞,m-1)递减,在(m-1,1)递减,在(1,+∞)递增,
即有x=1处取得最小值,且为2-2m.
则有h(m)=$\left\{\begin{array}{l}{2-2m,m≤2}\\{{m}^{2}-6m+6,2<m<4}\\{2m-10,m≥4}\end{array}\right.$'
(3)当m≥4时,h(m)<1即为2m-10<1,即m<$\frac{11}{2}$,
即有4≤m<$\frac{11}{2}$;
当2<m<4时,m2-6m+6<1解得1<m<5,即为2<m<4;
当m≤2时,2-2m<1可得m>$\frac{1}{2}$,即为$\frac{1}{2}$<m≤2.
综上可得$\frac{1}{2}$<m<$\frac{11}{2}$.
即不等式的解集为($\frac{1}{2}$,$\frac{11}{2}$).
点评 本题考查二次不等式恒成立问题的解法和解析式的求法,考查分类讨论的思想方法和不等式的解法,考查运算能力,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
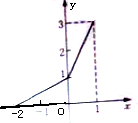 函数f(x)的图象是由两条线段组成的折线段(如图所示),则函数f(x)的表达式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.
函数f(x)的图象是由两条线段组成的折线段(如图所示),则函数f(x)的表达式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x+1,-2≤x≤0}\\{2x+1,0≤x≤1}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com