
【题目】如图,在四棱锥 A﹣BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4. 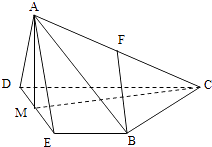
(1)求证:平面 ADE⊥平面BCD;
(2)求证:FB∥平面ADE;
(3)求四棱锥A﹣BCDE的体积.
【答案】
(1)证明:∵△AD E是等边三角形,M是D E的中点,
∴AM⊥DE, ![]() ,
,
∵在△DMC中,DM=1,∠CDM=60°,CD=4,
∴MC2=42+12﹣2×4×1×cos60°=13,
∴ ![]() ,
,
∵在△AMC中,A M2+MC2=3+13=16=AC2,
∴AM⊥MC,
∵MC∩DE=M,MC平面BCD,DE平面BCD,
∴AM⊥平面BCD,
∵AM平面ADE,
∴平面ADE⊥平面BCD
(2)证明:分别取AD,DC的中点G,N,连接FG,GE,FN,NB.
∵AC=DC,F,NF分别为AC,DC的中点,
∴ ![]() ,∴
,∴ ![]() ,
,
∴FN ![]() DN,
DN,
∴四边形DNFG是平行四边形,
∴ ![]() ,
,
∵点N是DC的中点,
∴BC=NC,又∠BCN=60°,
∴△BCN是等边三角形,
∴∠CNB=∠CDE=60°,
∴ ![]() ,
,
∴四边形EBND是平行四边形,
∴ ![]() ,
,
∴ ![]() ,
,
又平面ADE,GE平面ADE,
∴FB∥平面ADE
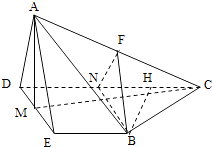
(3)解:过点B作BH⊥NC于点H,则BH= ![]() =
= ![]() =
= ![]() .
.
由(2)可知:四边形EBND是平行四边形,
∴EB=ND=2,
∴底面等腰梯形BCDE的面积S四边形EBCD= ![]() =3
=3 ![]() ,
,
∴四棱锥A﹣BCDE的体积V= ![]() =
= ![]() =3.
=3.
【解析】(1)利用等边三角形的性质可得AM⊥DE,在△DMC中,利用余弦定理可得MC2=13,利用勾股定理的逆定理可得:AM⊥MC,再利用线面垂直与面面垂直的判定定理即可证明.(2)分别取AD,DC的中点G,N,连接FG,GE,FN,NB.利用三角形中位线定理与平行四边形的性质可得: ![]() ,可得△BCN是等边三角形,可得四边形EBND是平行四边形,
,可得△BCN是等边三角形,可得四边形EBND是平行四边形, ![]() ,
, ![]() ,可得FB∥平面ADE;(3)过点B作BH⊥NC于点H,可得BH.又EB=ND=2,利用四棱锥A﹣BCDE的体积V=
,可得FB∥平面ADE;(3)过点B作BH⊥NC于点H,可得BH.又EB=ND=2,利用四棱锥A﹣BCDE的体积V= ![]() ,即可得出.
,即可得出.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个面垂直.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入的部分数据如表:
)在某一个周期内的图象时,列表并填入的部分数据如表:
x |
|
| |||
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | ﹣2 |
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)当x∈[0, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在正实数
,如果存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的“
上的“![]() 的型增函数”,已知
的型增函数”,已知![]() 是定义在
是定义在![]() 上的奇函数,且在
上的奇函数,且在![]() 时,
时, ![]() ,若
,若![]() 为
为![]() 上的“2017的型增函数”,则实数
上的“2017的型增函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=Asin(wx+φ)(A>0,w>0)上的一个最高点的坐标为( ![]() ,
, ![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点( ![]() π,0),φ∈(﹣
π,0),φ∈(﹣ ![]() ,
, ![]() ).
).
(1)求这条曲线的函数解析式;
(2)求函数的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示直角梯形ABCD中,AB∥DC,∠A=90°,AB=AD=2DC=4,画出该梯形的直观图A′B′C′D′,并写出其做法(要求保留作图过程的痕迹.)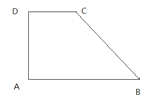
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|3≤3x≤27}, ![]() .
.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com