
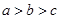 且
且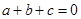 ,则
,则 ”是真命题还是假命题,并证明你的结论.
”是真命题还是假命题,并证明你的结论. 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:不详 题型:单选题
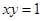 ,则
,则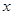 、
、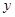 互为倒数”的逆命题;②“面积相等的两个三角形全等”的否命题;③“若
互为倒数”的逆命题;②“面积相等的两个三角形全等”的否命题;③“若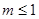 ,则
,则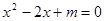 有实数根”的逆否命题;④“若
有实数根”的逆否命题;④“若 ”的逆否命题。其中正确的是( )
”的逆否命题。其中正确的是( )| A.①② | B.②③ | C.①②③ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
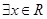 ,使得
,使得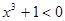 ”的否定是“
”的否定是“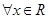 ,都有
,都有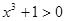 ”.
”.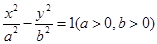 中,F为右焦点,
中,F为右焦点,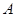 为左顶点,点
为左顶点,点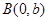 且
且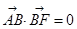
 ,则此双曲线的离心率为
,则此双曲线的离心率为 .
.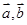 是夹角为
是夹角为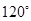 的单位向量,则向量
的单位向量,则向量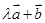 与
与 垂直的充要条件是
垂直的充要条件是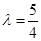 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
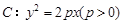 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设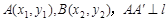 于
于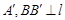 于
于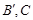 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②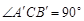 ;
; 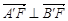 ; ④
; ④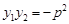 ; ⑤.
; ⑤. 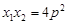
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
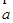 ∥
∥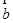
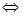 存在唯一的实数
存在唯一的实数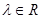 ,使得
,使得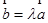 ;
;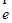 为单位向量,且
为单位向量,且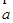 ∥
∥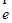 ,则
,则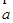 =±|
=±|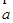 |·
|·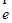 ;③
;③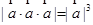 ;
;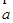 与
与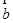 共线,
共线,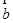 与
与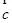 共线,则
共线,则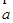 与
与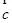 共线;⑤若
共线;⑤若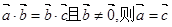
| A.①⑤ | B.②③④ |
| C.②③ | D.①④⑤ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
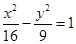 与椭圆
与椭圆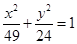 有相同的焦点;
有相同的焦点;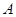 、
、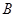 为两个定点,
为两个定点,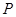 为动点,且
为动点,且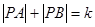 ,其中常数
,其中常数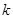 为正实数,则动点
为正实数,则动点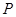 的轨迹为椭圆;
的轨迹为椭圆;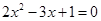 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;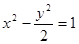 的右焦点
的右焦点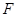 作直线
作直线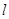 交双曲线于
交双曲线于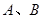 两点,若
两点,若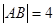 ,则这样的直线
,则这样的直线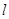 有且仅有3条。
有且仅有3条。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com