
【题目】设Sn为数列{an}的前n项和.已知![]() .
.
(Ⅰ)求{an}的通项公式;
(Ⅱ)令![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】(Ⅰ)an=2n+1;(Ⅱ)![]() .
.
【解析】
(Ⅰ)依题意有an2+2an=4Sn+3①,当n≥2时an-12+2an-1=4Sn-1+3②,两式对应相减an-an-1-2=0(n≥2),再利用等差数列的通项求{an}的通项公式;(Ⅱ)由题得![]() =
=![]() (
(![]() -
-![]() ),再利用裂项相消法求数列{bn}的前n项和Tn.
),再利用裂项相消法求数列{bn}的前n项和Tn.
(Ⅰ)依题意有an2+2an=4Sn+3①
当n=1时a12+2a1=4S1+3,解得a1=3,
当n≥2是an-12+2an-1=4Sn-1+3②,
①-②得(an+an-1)(an+an-1-2)=0,
∵an>0,
∴an+an-1>0,
∴an-an-1-2=0(n≥2),
∴{an}成等差数列,得an=3+2(n-1)=2n+1.
(Ⅱ)![]() =
=![]() =
=![]() =
=![]() (
(![]() -
-![]() ),
),
∴数列{bn}的前n项和Tn=![]() (1-
(1-![]() +
+![]() +…+
+…+![]() -
-![]() )=
)=![]() (1-
(1-![]() )=
)=![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆上.
在椭圆上.
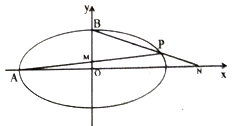
(1)求椭圆C的标准方程;
(2)设点P是椭圆C上一点,左顶点为A,上顶点为B,直线PA与y轴交于点M,直线PB与x轴交于点N,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】—般地,若函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,则称
,则称![]() 为
为![]() 的“
的“![]() 倍跟随区间”;特别地,若函数
倍跟随区间”;特别地,若函数![]() 的定义域为
的定义域为![]() ,值域也为
,值域也为![]() ,则称
,则称![]() 为
为![]() 的“跟随区间”.下列结论正确的是( )
的“跟随区间”.下列结论正确的是( )
A.若![]() 为
为![]() 的跟随区间,则
的跟随区间,则![]()
B.函数![]() 不存在跟随区间
不存在跟随区间
C.若函数![]() 存在跟随区间,则
存在跟随区间,则![]()
D.二次函数![]() 存在“3倍跟随区间”
存在“3倍跟随区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用给人民群众的健康带来了一定的危害.为了给消费者带来放心的蔬菜,某农村合作社每年投入资金![]() 万元,搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入资金
万元,搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入资金![]() 万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的种菜经验,发现种西红柿的年收入
万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的种菜经验,发现种西红柿的年收入![]() 、种黄瓜的年收入
、种黄瓜的年收入![]() 与各自的资金投入
与各自的资金投入![]() (单位:万元)满足
(单位:万元)满足![]() ,
,![]() .设甲大棚的资金投入为
.设甲大棚的资金投入为![]() (单位:万元),每年两个大棚的总收入为
(单位:万元),每年两个大棚的总收入为![]() (单位:万元).
(单位:万元).
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的资金投入,才能使总收入![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用 “健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 九组,整理得到如下频率分布直方图:
九组,整理得到如下频率分布直方图:
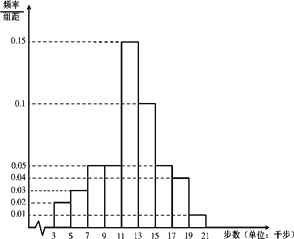
(Ⅰ)求当天这1000名会员中步数少于11千步的人数;
(Ⅱ)从当天步数在![]() ,
, ![]() ,
, ![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(Ⅲ)写出该组数据的中位数(只写结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直![]() :x+my-2m=0与动直线
:x+my-2m=0与动直线![]() :mx-y-4m+2=0相交于点M,记动点M的轨迹为曲线C.
:mx-y-4m+2=0相交于点M,记动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点P(-1,0)作曲线C的两条切线,切点分别为A,B,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com