
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| c |
| b |
| c |
A、以
| ||||
B、以
| ||||
C、以
| ||||
D、以
|
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| a |
| c |
| a |
| c |
| OA |
| a |
| OB |
| b |
| OC |
| c |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| T8 |
| T4 |
| T12 |
| T8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| δ | 2 1 |
| δ | 2 2 |
查看答案和解析>>
科目:高中数学 来源:2015届广东省佛山市高一下学期期中考试数学试卷(解析版) 题型:选择题
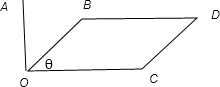
设 、
、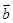 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与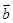 不共线,
不共线,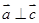 ,
, ,则
,则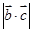 的值一定等于( )
的值一定等于( )
A.以 、
、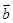 为两边的三角形面积; B.以
为两边的三角形面积; B.以 、
、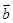 为邻边的平行四边形的面积;
为邻边的平行四边形的面积;
C.以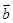 、
、 为两边的三角形面积; D.以
为两边的三角形面积; D.以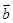 、
、 为邻边的平行四边形的面积.
为邻边的平行四边形的面积.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市高三毕业班质量检查文科数学试卷(解析版) 题型:选择题
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为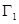 ;由同时满足
;由同时满足 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到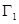 的体积为
的体积为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com