
【题目】下列函数中,在其定义域内既是奇函数又是单调递增的函数是( )
A.y=﹣ ![]()
B.y=3﹣x﹣3x
C.y=x|x|
D.y=x3﹣x
【答案】C
【解析】解:对于A,y= ![]() 的定义域为{x|x≠0},是奇函数,但在定义域上不单调,不满足条件;
的定义域为{x|x≠0},是奇函数,但在定义域上不单调,不满足条件;
对于B,y=3﹣x﹣3x的定义域为R,奇函数,是定义域上单调减函数,不满足条件;
对于C,y=x|x|的定义域为R,满足f(﹣x)=﹣f(x),是奇函数,是定义域R上的单调增函数,满足题意;
对于D,f(x)=x3﹣x的定义域为R,满足f(﹣x)=﹣f(x),是奇函数,在R上不是单调函数,不满足条件.
故选:C.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和函数的奇偶性的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温/℃ | 18 | 13 | 10 | -1 |
用电量/度 | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程![]() 中,
中,![]() ≈-2,预测当气温为-4℃时,用电量为多少.
≈-2,预测当气温为-4℃时,用电量为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|.
(1)当a=3时,求不等式f(x)≥2的解集;
(2)若f(x)≥5﹣x对x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin2x+1﹣
sin2x+1﹣ ![]() .
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,若f(x)≥log2t恒成立,求t的取值范围.
]时,若f(x)≥log2t恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
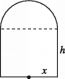
【题目】某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
(1)写出S关于x的函数关系式;
(2)如何设计瓶子的尺寸(不考虑瓶壁的厚度),可以使表面积S最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋中装有n个红球(n≥1且n∈N+)和2个白球,从中有放回地连续摸三次,每次摸出2个球,若2个球颜色不同则为中奖,否则不中奖.
(1)当n=3时,设三次摸球中中奖的次数为X,求随机变量X的分布列;
(2)记三次摸球中恰有两次中奖的概率为P,求当n取多少时,P的值最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com