
解答须写出文字说明、证明过程和演算步骤.
若椭圆![]() 过点(-3,2),离心率为
过点(-3,2),离心率为![]() ,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;
(Ⅲ)求![]() 的最大值与最小值.
的最大值与最小值.
科目:高中数学 来源:2008年天河区理科数学模拟卷(一) 题型:044
解答须写出文字说明、证明过程和演算步骤.
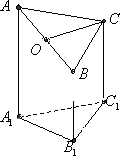
下图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3
(Ⅰ)设点O是AB的中点,证明:OC∥平面A1B1C1
(Ⅱ)求AB与平面AA1CC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2008年天河区理科数学模拟卷(一) 题型:044
解答须写出文字说明、证明过程和演算步骤.
某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
(Ⅰ)求年推销金额y与工作年限x之间的相关系数;
(Ⅱ)求年推销金额y关于工作年限x的线性回归方程;
(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.

(参考数据:![]() ;由检验水平0.01及n-2=3,查表得γ0.01=0.959.
;由检验水平0.01及n-2=3,查表得γ0.01=0.959.
![]() =10,
=10,![]() 20,
20,![]() 5.2,)
5.2,)
查看答案和解析>>
科目:高中数学 来源:2008年天河区理科数学模拟卷(一) 题型:044
解答须写出文字说明、证明过程和演算步骤.
设函数![]() 在其图象上一点P(x,y)处的切线的的斜率记为f(x).
在其图象上一点P(x,y)处的切线的的斜率记为f(x).
(Ⅰ)若方程f(x)=0有两个实根分别为-2和4,求![]() ;
;
(Ⅱ)若![]() 在区间[-1,3]上是单调递减函数,求a2+b2的最小值.
在区间[-1,3]上是单调递减函数,求a2+b2的最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省汕头市高二下学期期末考试文科数学 题型:解答题
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
 16.(本小题满分12分)[来源:学§科§网]
16.(本小题满分12分)[来源:学§科§网]
已知函数 的最大值是2,其图象经过点
 .
.
(1)求 的解析式;
的解析式;
(2)已知 ,且
,且 ,
,
求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com