
【题目】一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是_____________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
【答案】18,05,07,35,59,26,39.
【解析】
从随机数表的倒数第5行第11~12列开始,依次向下,到最后一行后向右读取两位数,大于等于60的数据应舍去,与前面取到的数据重复的也舍去,直到取足7个样本号码为止.
解:根据题意,60个个体编号为00,01,![]() ,59,现从中抽取一容量为7的样本,
,59,现从中抽取一容量为7的样本,
从随机数表的倒数第5行第11~12列开始,向下读取,到最后一行后向右
18,81(舍去),90(舍去),82(舍去),05,98(舍去),90(舍去),07,35,82(舍去),96(舍去),59,26,94(舍去),66(舍去),39共7个;
所以抽取样本的号码是18,00,46,40,54,20,56.
故答案为:18,05,07,35,59,26,39.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求函数![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .(Ⅱ)当
.(Ⅱ)当![]() 时,
时, ![]()
![]() ;当
;当![]() 时,
时, ![]()
![]() .
.
【解析】【试题分析】(I)利用![]() 的二阶导数来研究求得函数
的二阶导数来研究求得函数![]() 的单调区间.(II) 由(Ⅰ)得
的单调区间.(II) 由(Ⅰ)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,由此可知
上单调递增,由此可知![]() .利用导数和对
.利用导数和对![]() 分类讨论求得函数在
分类讨论求得函数在![]() 不同取值时的最大值.
不同取值时的最大值.
【试题解析】
(Ⅰ)![]() ,
,
设![]()
![]() ,则
,则![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
从而得![]() 在
在![]() 上单调递增,又∵
上单调递增,又∵![]() ,
,
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
因此, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
设![]() ,
,
则![]()
![]()
 .
.
∵当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
①当![]() 时,
时, ![]() ,即
,即![]() ,这时,
,这时, ![]()
![]() ;
;
②当![]() 时,
时, ![]() ,即
,即![]() ,这时,
,这时, ![]()
![]() .
.
综上, ![]() 在
在![]() 上的最大值为:当
上的最大值为:当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() .
.
[点睛]本小题主要考查函数的单调性,考查利用导数求最大值. 与函数零点有关的参数范围问题,往往利用导数研究函数的单调区间和极值点,并结合特殊点,从而判断函数的大致图像,讨论其图象与![]() 轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
【题型】解答题
【结束】
22
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() . 在以坐标原点为极点,
. 在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ) 写出圆 ![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
( Ⅱ ) 设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 任作一直线交抛物线
任作一直线交抛物线![]() 于
于![]() 两点,过
两点,过![]() 两点分别作抛物线的切线
两点分别作抛物线的切线![]() .
.
(Ⅰ)记![]() 的交点
的交点![]() 的轨迹为
的轨迹为![]() ,求
,求![]() 的方程;
的方程;
(Ⅱ)设![]() 与直线
与直线![]() 交于点
交于点![]() (异于点
(异于点![]() ),且
),且![]() ,
,![]() .问
.问![]() 是否为定值?若为定值,请求出定值.若不为定值,请说明理由.
是否为定值?若为定值,请求出定值.若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一个总体的100个个体编号为0,1,2,…,99,并依次将其分为10个组,组号为0,1,2,…,9.要用系统抽样法抽取一个容量为10的样本,如果在第0组(号码为0—9)随机抽取的号码为2,则抽取的10个号码为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学期开展覆盖本校各年级学生的《标准》测试工作,并根据学生每个学期总分评定等级.某校决定针对高中学生,每学期进行一次体质健康测试,以下是小明同学六个学期体质健康测试的总分情况.
学期 | 1 | 2 | 3 | 4 | 5 | 6 |
总分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)请根据上表提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度,并用最小二乘法求出
的线性相关程度,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程(线性相关系数保留两位小数);
的线性回归方程(线性相关系数保留两位小数);
(2)在第六个学期测试中学校根据 《标准》,划定540分以上为优秀等级,已知小明所在的学习小组10个同学有6个被评定为优秀,测试后同学们都知道了自己的总分但不知道别人的总分,小明随机的给小组内4个同学打电话询问对方成绩,优秀的同学有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
参考公式: 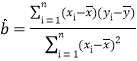 ,
,![]() ;
;
相关系数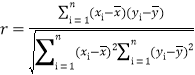 ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=![]() ,其中2<m<2,m∈Z,满足:
,其中2<m<2,m∈Z,满足:
(1)f(x)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(x) +f(x)=0.
求同时满足条件(1)、(2)的幂函数f(x)的解析式,并求x∈[0,3]时,f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)当直线![]() 与椭圆
与椭圆![]() 相切,交
相切,交![]() 于点
于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的直线方程.
的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com