Question

【题目】为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有800名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩进行统计． 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：

分组	频数	频率
50.5～60.5	6	0.08
60.5～70.5		0.16
70.5～80.5	15
80.5～90.5	24	0.32
90.5～100.5
合计	75	1.00

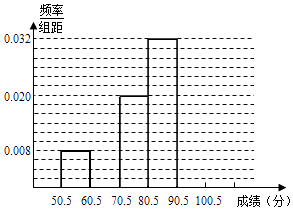
（1）填充频率分布表的空格；
（2）补全频率分布直方图；
（3）根据频率分布直方图求此次“环保知识竞赛”的平均分为多少？

Answer 1

【答案】
（1）解：

分组	频数	频率
50.5～60.5	6	0.08
60.5～70.5	12	0.16
70.5～80.5	15	0.20
80.5～90.5	24	0.32
90.5～100.5	18	0.24
合计	75	1.00

（2）解：如图所示：

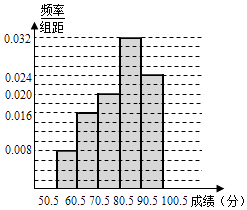
（3）解：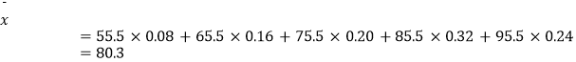

∴此次“环保知识竞赛”的平均分为80.30（分）

【解析】（1）根据频率= ，分别计算即可，（2）由统计表补全直方图即可，（3）利用组中值乘以对应的频率即可估计环保知识竞赛”的平均分．
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息，以及对平均数、中位数、众数的理解，了解⑴平均数、众数和中位数都是描述一组数据集中趋势的量；⑵平均数、众数和中位数都有单位；⑶平均数反映一组数据的平均水平，与这组数据中的每个数都有关系，所以最为重要，应用最广；⑷中位数不受个别偏大或偏小数据的影响；⑸众数与各组数据出现的频数有关，不受个别数据的影响，有时是我们最为关心的数据．