练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，射线OA、OB分别与x轴、y轴所成的角均为30°，已知线段PQ的长度为2，并且保持线段的端点P(x1，y1)在射线OA上运动，Q(x2，y2)在射线OB上运动．

     

    　　(1)试求点M(x1，x2)的轨迹C的方程；

     

    　　(2)求轨迹C上的动点N到直线x-y-3=0的距离的最大值和最小值．

     

    答案：
    解析：

    解：(1)设M(x，y)，则有：

    　　

    　　整理得：，x≥0，y≤0

    　　(2)设N(cosq，sinq)，≤q≤0

    　　N到直线x-y-3=0的距离为：

    　　

    　　　

    　　∵　≤q≤0

    　　∴　

    　　∴　，

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

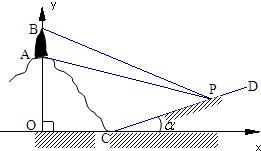    精英家教网如图所示，某人在斜坡P处仰视正对面山顶上一座铁塔，塔高AB=80米，塔所在山高OA=220米，OC=200米，观测者所在斜坡CD近似看成直线，斜坡与水平面夹角为α，tanα=
    12

    （1）以射线OC为Ox轴的正向，OB为Oy轴正向，建立直角坐标系，求出斜坡CD所在直线方程；
    （2）当观察者P视角∠APB最大时，求点P的坐标（人的身高忽略不计）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，四边形OABP是平行四边形，过点P的直线与射线OA、OB分别相交于点M、N，若 
    OM
    =x
    OA
    ，
    ON
    =y
    OB

    （1）利用
    NM
    ∥
    MP
    ，把y用x表示出来（即求y=f（x）的解析式）；
    （2）设数列{an}的首项a1=1，前 n项和Sn满足：Sn=f（Sn-1）（n≥2），求数列{an}通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，两射线OA与OB交于O，下列向量若以O为起点，终点落在阴影区域内（含边界）的是
    ②
    ②
    ．
    ①2
    OA
    -
    OB
    ；
    ②
    3
    4
    OA
    +
    1
    3
    OB
    ；
    ③
    1
    2
    OA
    +
    1
    3
    OB
    ；
    ④
    3
    4
    OA
    +
    1
    5
    OB
    ；
    ⑤
    3
    4
    OA
    -
    1
    5
    OB
    ．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如图所示，射线OA、OB分别与x轴、y轴所成的角均为30°，已知线段PQ的长度为2，并且保持线段的端点P(x1，y1)在射线OA上运动，Q(x2，y2)在射线OB上运动．

     

    　　(1)试求点M(x1，x2)的轨迹C的方程；

     

    　　(2)求轨迹C上的动点N到直线x-y-3=0的距离的最大值和最小值．

     

    查看答案和解析>>

    同步练习册答案