
【题目】已知![]() .
.
(I)讨论![]() 的单调性;
的单调性;
(II)当![]() 有最大值,且最大值大于
有最大值,且最大值大于![]() 时,求a的取值范围.
时,求a的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ)![]()
【解析】试题分析:
(1)由题已知函数的解析式(注意定义域),可运用导数求出函数的单调区间。即: ![]() 为函数的增区间,反之为减区间。由导函数中含有字母参数,需分类讨论;
为函数的增区间,反之为减区间。由导函数中含有字母参数,需分类讨论;
(2)由题给出了函数的最大值的范围大于![]() ,再结合(1)已知函数的单调区间,可对应单调性,表示出函数的最大值,从而建立不等式lna+a-1<0,需构造函数利用单调性解出不等式的解,而求出
,再结合(1)已知函数的单调区间,可对应单调性,表示出函数的最大值,从而建立不等式lna+a-1<0,需构造函数利用单调性解出不等式的解,而求出![]() 的取值范围。
的取值范围。
试题解析:
(Ⅰ)f(x)=lnx+a(1﹣x)的定义域为(0,+∞),∴f′(x)=![]() ﹣a=
﹣a=![]() ,
,
若a≤0,则f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,
若a>0,则当x∈(0,![]() )时,f′(x)>0,
)时,f′(x)>0,
当x∈(![]() ,+∞)时,f′(x)<0,所以f(x)在(0,
,+∞)时,f′(x)<0,所以f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减,
,+∞)上单调递减,
(Ⅱ)由(Ⅰ)知,当a≤0时,f(x)在(0,+∞)上无最大值;
当a>0时,f(x)在x=![]() 取得最大值,最大值为f(
取得最大值,最大值为f(![]() )=﹣lna+a-1,
)=﹣lna+a-1,
∵f(![]() )>2a﹣2,∴lna+a-1<0,
)>2a﹣2,∴lna+a-1<0,
令g(a)=lna+a-1,∵g(a)在(0,+∞)单调递增,g(1)=0,
∴当0<a<1时,g(a)<0,当a>1时,g(a)>0,∴a的取值范围为(0,1).


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为 ![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x2+ax﹣a﹣1),给出下列命题:
①函数f(x)有最小值;
②当a=0时,函数f(x)的值域为R;
③若函数f(x)在区间(﹣∞,2]上单调递减,则实数a的取值范围是a≤﹣4.
其中正确的命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若以曲线![]() 上任意一点
上任意一点![]() 为切点作切线
为切点作切线![]() ,曲线上总存在异于
,曲线上总存在异于![]() 的点
的点![]() ,以点
,以点![]() 为切点作切线
为切点作切线![]() ,且
,且![]() ,则称曲线
,则称曲线![]() 具有“可平行性”,现有下列命题:
具有“可平行性”,现有下列命题:
①函数![]() 的图象具有“可平行性”;
的图象具有“可平行性”;
②定义在![]() 的奇函数
的奇函数![]() 的图象都具有“可平行性”;
的图象都具有“可平行性”;
③三次函数![]() 具有“可平行性”,且对应的两切点
具有“可平行性”,且对应的两切点![]() ,
, ![]() 的横坐标满足
的横坐标满足![]() ;
;
④要使得分段函数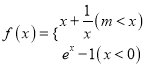 的图象具有“可平行性”,当且仅当
的图象具有“可平行性”,当且仅当![]() .
.
其中的真命题个数有()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
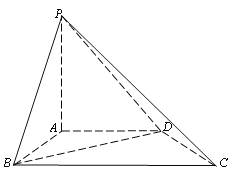
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com