
【题目】某大型科学竞技真人秀节目挑选选手的方式为:不但要对选手的空间感知、照相式记忆能力进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有95%以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,求这11名学生中男、女生人数;若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),分别求这11名学生中女生测试分数平均分的最小值.
|
|
|
|
|
|
|
|
|
|
附: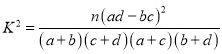 ,其中
,其中![]() .
.
【答案】(1)见解析,没有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关;(2)女生5人,男生6人,122.
以上的把握认为脑力测试后是否为“入围学生”与性别有关;(2)女生5人,男生6人,122.
【解析】
(1)根据题意,填写列联表.根据参考公式,计算![]() 的观测值,再根据临界值表,即得结论;
的观测值,再根据临界值表,即得结论;
(2)根据分层抽样原理计算被抽到的女生人数,即得被抽到的男生人数.根据题意,被抽到的女生测试分数的平均分最小时,这5名女生的测试分数分别为![]() ,即可求平均分的最小值.
,即可求平均分的最小值.
(1)填写列联表如下:
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | 76 | 100 |
女生 | 20 | 80 | 100 |
总计 | 44 | 156 | 200 |
![]() 的观测值
的观测值![]()
所以没有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关.
以上的把握认为脑力测试后是否为“入围学生”与性别有关.
(2)在这11名学生中,被抽到的女生人数为![]() (人),
(人),
被抽到的男生人数为![]() (人)或
(人)或![]() (人).
(人).
因为入围的分数不低于120分,且每个女生的测试分数各不相同,每个人的分数都是整数.
所以这11名学生中女生测试分数的平均分的最小值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为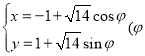 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 的交线为直线
的交线为直线![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】仔细观察数列给出部分的数字,寻找规律,在空白处填上合适的数字.
(1)2,3,5,8,__________21;(2)8,_______14,17,20,23;
(3)2,4,8,16,_______,64;(4)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,_________.
,_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点纵坐标伸长到原来的2倍(横坐标不变)得到曲线
上各点纵坐标伸长到原来的2倍(横坐标不变)得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() ,
,![]() (以上两点坐标均为极坐标,
(以上两点坐标均为极坐标,![]() ,
,![]() ),使点
),使点![]() 、
、![]() 到
到![]() 的距离都为3?若存在,求
的距离都为3?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆C满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>0,0≤x<2π,若函数y=cos2x-asinx+b的最大值为0,最小值为-4,试求a与b的值,并求使y取得最大值和最小值时的x值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com