
分析 (1)运用代入法,结合对数运算法则,即可得到所求值;
(2)运用对数函数的单调性,可得t的范围,化简可得g(t)的解析式,且g(t)在[2,3]上递增,运用单调性的定义证明,注意取值,作差,变形,定符号和下结论等步骤;
(3)由题意可得a≤g(t)的最小值,由(2)的单调性,可得g(2)最小,可得a的范围.
解答 解:(1)函数f(x)=log2(2x)•log2(4x),
可得f($\sqrt{2}$)=log2(2$\sqrt{2}$)•log2(4$\sqrt{2}$)
=log22${\;}^{\frac{3}{2}}$•log22${\;}^{\frac{5}{2}}$=$\frac{3}{2}$×$\frac{5}{2}$=$\frac{15}{4}$;
(2)t=log2x(4≤x≤8),
可得2≤t≤3,
g(t)=$\frac{f(x)}{t}$-3=$\frac{(1+lo{g}_{2}x)(2+lo{g}_{2}x)}{t}$-3
=$\frac{(1+t)(2+t)}{t}$-3=$\frac{{t}^{2}+2}{t}$
=t+$\frac{2}{t}$,(2≤t≤3).
结论:g(t)在[2,3]上递增.
理由:设2≤t1<t2≤3,
则g(t1)-g(t2)=t1+$\frac{2}{{t}_{1}}$-(t2+$\frac{2}{{t}_{2}}$)=(t1-t2)+$\frac{2({t}_{2}-{t}_{1})}{{t}_{1}{t}_{2}}$
=(t1-t2)•$\frac{{t}_{1}{t}_{2}-2}{{t}_{1}{t}_{2}}$,
由2≤t1<t2≤3,可得t1-t2<0,t1t2>4>2,
即有g(t1)-g(t2)<0,
则g(t)在[2,3]上递增.
(3)a≤g(t)恒成立,
即为a≤g(t)的最小值.
由g(t)在[2,3]上递增,
可得g(2)取得最小值,且为3.
则实数a的取值范围为a≤3.
点评 本题考查函数的解析式的求法,以及单调性的判断和证明,注意运用定义法,同时考查恒成立问题的解法,注意运用函数的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
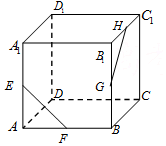 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,0),(4,0) | B. | (-3,0),(3,0) | C. | (0,-4),(0,4) | D. | (0,-3),(0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com