
【题目】已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线. 
(1)求∠BAE 的度数;
(2)求证: ![]()
【答案】
(1)解:在△EAB与△ECA中,∵AE为圆O的切线,
∴∠EBA =∠EAC
又∠E公用,∴∠EAB =∠ECA
∵△ACD为等边三角形,
∴
(2)证明:∵AE为圆O的切线,
∴∠ABD=∠CAE
∵△ACD为等边三角形,
∴∠ADC =∠ACD,
∴∠ADB=∠ECA,
∴△ABD∽△EAC
∴ ,即
∵△ACD为等边三角形,
∴AD=AC=CD,
∴ ![]()
【解析】分析:本题主要考查了圆的切线的性质及判定定理,解决问题的关键是(1)在△EAB与△ECA中,因为AE为圆O的切线,所以∠EBA =∠EAC,∠EAB =∠ECA,因为△ACD为等边三角形,所以 ![]() ;(2)容易证明△ABD∽△EAC ,所以
;(2)容易证明△ABD∽△EAC ,所以 ![]() ,即
,即 ![]() ,因为△ACD为等边三角形,所以AD=AC=CD,所以
,因为△ACD为等边三角形,所以AD=AC=CD,所以 ![]()


科目:高中数学 来源: 题型:
【题目】下表是一位母亲给儿子作的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据,她建立了身高 ![]() (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为 ![]() ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是 ![]() cm;
cm;
④儿子年龄增加1周岁,身高约增加 ![]() cm.
cm.
其中,正确结论的个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的![]() 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0 | 2001 | 5001 | 8001 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的![]() 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: 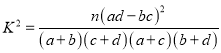
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D,E,F分别为△ABC的边BC,CA,AB的中点,记 ![]() =a ,
=a , ![]() =b.则下列命题中正确的个数是( )
=b.则下列命题中正确的个数是( )
① ![]() =
= ![]() a-b;②
a-b;② ![]() =a+
=a+ ![]() b;③
b;③ ![]() =
= ![]() a+
a+ ![]() b;④
b;④ ![]() 0.
0.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com