【题目】2018年11月6日-11日，第十二届中国国际航空航天博览会在珠海举行。在航展期间，从珠海市区开车前往航展地有甲、乙两条路线可走，已知每辆车走路线甲堵车的概率为
，走路线乙堵车的概率为p，若现在有A，B两辆汽车走路线甲，有一辆汽车C走路线乙，且这三辆车是否堵车相互之间没有影响。
（1）若这三辆汽车中恰有一辆汽车被堵的概率为
，求p的值。
（2）在（1）的条件下，求这三辆汽车中被堵车辆的辆数X的分布列和数学期望。
科目：高中数学 来源： 题型：
【题目】如图，已知双曲线
的两条渐近线分别为
.
为坐标原点，动直线
分别交直线
于
两点(分别在第一四象限)，且
的面积恒为8.试探究：是否存在总与直线有且只有一个公共点的双曲线
？若存在，求出双曲线的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种常见疾病可分为Ⅰ、Ⅱ两种类型.为了解该疾病类型与地域、初次患该疾病的年龄（以下简称初次患病年龄）的关系，在甲、乙两个地区随机抽取100名患者调查其疾病类型及初次患病年龄，得到如下数据：
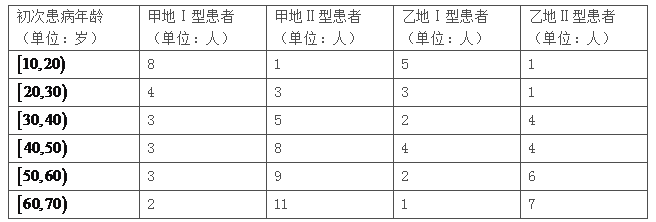
（1）从Ⅰ型疾病患者中随机抽取1人，估计其初次患病年龄小于40岁的概率；
（2）记“初次患病年龄在
的患者为“低龄患者”，初次患病年龄在
的患者为“高龄患者”，根据表中数据，解决以下问题：
将以下两个列联表补充完整，并判断“地域”“初次患病年龄”这两个变量中哪个变量与该疾病的类型有关联的可能性更大.（直接写出结论，不必说明理由）
（ii）记（i）中与该疾病的类型有关联的可能性更大的变量为
，问：是否有99.9%的把握认为“该疾病的类型与有关？”
附：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数 f（x）=ax+（1﹣a）lnx+
（a∈R）
（Ⅰ）当a=0时，求 f（x）的极值；
（Ⅱ）当a＜0时，求 f（x）的单调区间；
（Ⅲ）方程 f（x）=0的根的个数能否达到3，若能请求出此时a的范围，若不能，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：如果数列
的任意连续三项均能构成一个三角形的三边长，则称为“三角形”数列，对于“三角形”数列，如果函数
使得
仍为一个“三角形”数列，则称是数列的“保三角形函数”
．
（1）已知是首项为2，公差为1的等差数列，若
是数列的“保三角形函数”，求k的取值范围；
（2）已知数列
的首项为2010，
是数列的前n项和，且满足
，证明是“三角形”数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的普通方程为
，以原点
为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（I）求的参数方程与的直角坐标方程；
（II）射线
与交于异于极点的点
,与的交点为
,求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥P﹣ABC中，AB＝1，BC＝2，AC
，PC
，PA，PB
，E是线段BC的中点．
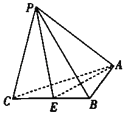
（1）求点C到平面APE的距离d；
（2）求二面角P﹣EA﹣B的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
