【题目】十二生肖是十二地支的形象化代表，即子（鼠）、丑（牛）、寅（虎）、卯（兔）、辰（龙）、巳（蛇）、午（马）、未（羊）、申（猴）、酉（鸡）、戌（狗）、亥（猪），每一个人的出生年份对应了十二种动物中的一种，即自己的属相.现有印着十二生肖图案的毛绒娃娃各一个，小张同学的属相为马，小李同学的属相为羊，现在这两位同学从这十二个毛绒娃娃中各随机取一个（不放回），则这两位同学都拿到自己属相的毛绒娃娃的概率是（ ）
A.
B.
C.
D.
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，以椭圆E的长轴和短轴为对角线的四边形的面积为
.
（1）求椭圆E的方程；
（2）若直线
与椭圆E相交于A，B两点，设P为椭圆E上一动点，且满足
（O为坐标原点）.当
时，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校周五的课程表设计中，要求安排8节课（上午4节下午4节），分别安排语文数学英语物理化学生物政治历史各一节，其中生物只能安排在第一节或最后一节，数学和英语在安排时必须相邻（注：上午的最后一节与下午的第一节不记作相邻），则周五的课程顺序的编排方法共有（ ）．
A.4800种B.2400种C.1200种D.240种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在平面直角坐标系
中，直线
（
为参数），以原点为极点，
轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线
的极坐标方程为
.
（1）求直线
的普通方程及曲线的直角坐标方程；
（2）设点
直角坐标为
，直线与曲线交于
，
两点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校2011年到2019年参加“北约”“华约”考试而获得加分的学生人数（每位学生只能参加“北约”“华约”中的一种考试）可以通过以下表格反映出来，（为了方便计算，将2011年编号为1，2012年编号为2，依此类推）
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数y | 2 | 3 | 5 | 4 | 5 | 7 | 8 | 10 | 10 |
（1）求这九年来，该校参加“北约”“华约”考试而获得加分的学生人数的平均数和方差；
（2）根据最近五年的数据，利用最小二乘法求出y与x的线性回归方程，并依此预测该校2020年参加“北约”“华约”考试而获得加分的学生人数．（最终结果精确至个位）
参考数据：回归直线的方程是
，其中
，
，
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，
，点
在椭圆
上，点
满足以
为直径的圆过椭圆的上顶点
.
（1）求椭圆的方程；
（2）已知直线
过右焦点
与椭圆交于
两点，在
轴上是否存在点
使得
为定值？如果存在，求出点
的坐标；如果不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业为确定下一年投入某种产品的研发费用，需了解年研发费用
（单位：千万元）对年销售量
（单位：千万件）的影响，统计了近10年投入的年研发费用
与年销售量
的数据，得到散点图如图所示：
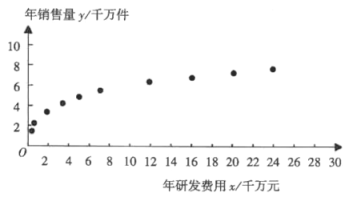
（1）利用散点图判断，
和
（其中
为大于0的常数）哪一个更适合作为年研发费用和年销售量的回归方程类型（只要给出判断即可，不必说明理由）.
（2）对数据作出如下处理：令
，
，得到相关统计量的值如下表：
根据（1）的判断结果及表中数据，求关于的回归方程；
（3）已知企业年利润
（单位：千万元）与
的关系为
（其中
），根据（2）的结果，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用？
附：对于一组数据
，
，
，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
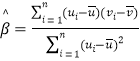查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面几个命题中，假命题是（ ）
A. “若
，则
”的否命题
B. “
，函数
在定义域内单调递增”的否定
C. “
是函数
的一个周期”或“
是函数
的一个周期”
D. “
”是“
”的必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
