
【题目】如图, ![]() 为圆柱
为圆柱![]() 的母线,
的母线, ![]() 是底面圆
是底面圆![]() 的直径,
的直径, ![]() 是
是![]() 的中点.
的中点.
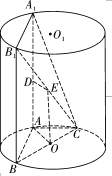
(Ⅰ)问: ![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?请说明理由;
?请说明理由;
(Ⅱ)在(Ⅰ)的条件下,若![]() 平面
平面![]() ,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥
,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥![]() 外会有被捕的危险,求小鱼被捕的概率.
外会有被捕的危险,求小鱼被捕的概率.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(Ⅰ)可先猜测E是![]() 的中点,再证明,由题意推导出四边形AOED是平行四边形,由此能证明DE∥平面ABC;
的中点,再证明,由题意推导出四边形AOED是平行四边形,由此能证明DE∥平面ABC;
(Ⅱ)鱼被捕的概率等于1减去四棱锥C-ABB1A1与圆柱OO1的体积比,由此求出四棱锥C-ABB1A1与圆柱OO1的体积,即可得出结果.
试题解析:
(Ⅰ)存在,E是![]() 的中点.
的中点.
证明:如图

连接![]() ∵
∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,
,
又![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
即![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)鱼被捕的概率![]() ,
,
由![]() 平面
平面![]() ,且由(Ⅰ)知
,且由(Ⅰ)知![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() 是
是![]() 中点,∴
中点,∴![]() ,因
,因![]() 是底面圆
是底面圆![]() 的直径,得
的直径,得![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高.
的高.
设圆柱高为![]() ,底面半径为
,底面半径为![]() ,则
,则![]() ,
,
![]() ,
,
∴![]() ∶
∶![]() ,即
,即![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.
(1)求抛物线的方程;
(2)过F的直线l与抛物线相交于A,D两点,与圆![]() 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[1,+∞)上的函数f(x)满足:①f(2x)=2f(x);②当2≤x≤4时,f(x)=1-|x-3|.则函数g(x)=f(x)-2在区间[1,28]上的零点个数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
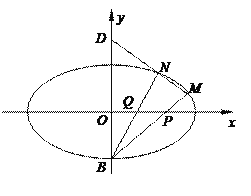
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的下顶点为
的下顶点为![]() ,点
,点![]() 是椭圆上异于点
是椭圆上异于点![]() 的动点,直线
的动点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 是线段
是线段![]() 的中点.当点
的中点.当点![]() 运动到点
运动到点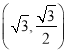 处时,点
处时,点![]() 的坐标为
的坐标为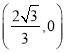 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 均在
均在![]() 轴右侧,且
轴右侧,且![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车因绿色、环保、健康的出行方式,在国内得到迅速推广.最近,某机构在某地区随机采访了10名男士和10名女士,结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”,其他人表示“较少或不选择骑共享单车出行”.
(1)从这些男士和女士中各抽取一人,求至少有一人“经常骑共享单车出行”的概率;
(2)从这些男士中抽取一人,女士中抽取两人,记这三人中“经常骑共享单车出行”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com