
【题目】已知函数f(x)=x2+1,g(x)=4x+1,的定义域都是集合A,函数f(x)和g(x)的值域分别为S和T,
(1)若A=[1,2],求S∩T
(2)若A=[0,m]且S=T,求实数m的值
(3)若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
【答案】(1)S∩T={5}.(2)m=4(3){0],或{4}或{0,4}.
【解析】
(1)根据定义域,求得两个函数的值域,再求交集即可;
(2)根据函数单调性,得![]() ,解方程即可;
,解方程即可;
(3)由题意,解方程f(x)=g(x)即可.
(1)若A=[1,2],
则函数f(x)=x2+1的值域是S=[2,5],
g(x)=4x+1的值域T=[5,9],
∴S∩T={5}.
(2)若A=[0,m],则S=[1,m2+1],T=[1,4m+1],
由S=T得m2+1=4m+1,
解得m=4或m=0(舍去).
故![]() .
.
(3)若对于A中的每一个x值,都有f(x)=g(x),
即x2+1=4x+1,
∴x2=4x,
解得x=4或x=0,
∴满足题意的集合是{0],或{4}或{0,4}.


科目:高中数学 来源: 题型:
【题目】给定![]() ,
,![]() ,
,![]() ,
,![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,
,![]() ,在
,在![]() 所在平面作直线
所在平面作直线![]() 与
与![]() 的某两边相交,沿
的某两边相交,沿![]() 将
将![]() 折成一个空间图形,将由
折成一个空间图形,将由![]() 分成的小三角形的不在
分成的小三角形的不在![]() 上的顶点与另一部分的顶点连接,形成一个三棱锥或四棱锥。问:
上的顶点与另一部分的顶点连接,形成一个三棱锥或四棱锥。问:
(1)当![]() 时,
时,![]() 如何作,并折成何种锥体,才能使所得锥体体积最大?(需详证)
如何作,并折成何种锥体,才能使所得锥体体积最大?(需详证)
(2)当![]() 时,
时,![]() 如何作,并折成何种锥体,才能使所得锥体体积最大?(叙述结果,不要证明)
如何作,并折成何种锥体,才能使所得锥体体积最大?(叙述结果,不要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,并整理得到频率分布直方图(如图所示).
,并整理得到频率分布直方图(如图所示).
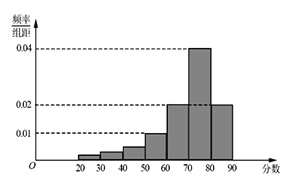
(Ⅰ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的人数.
内的人数.
(Ⅱ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
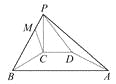
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点P
,且经过点P![]() ,过它的左、右焦点
,过它的左、右焦点![]() 分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且
分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且![]()
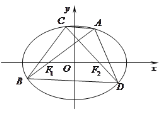
(1)求椭圆的标准方程.
(2)求四边形ACBD的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】游乐场的摩天轮匀速旋转,其中心O距地面40.5m,半径40m.若从最低点处登上座天轮,那么人与地面的距离将随时间变化,5min后达到最高点,在你登上摩天轮时开始计时,
(1)求出人与地面距离y与时间t的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于20.5m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,且
,且![]() .
.
(1)定义:对于函数![]() ,若存在
,若存在![]() ,使
,使![]() ,则称
,则称![]() 是
是![]() 的一个不动点;
的一个不动点;
(i)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(ii)对任意实数b,函数![]() 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(2)求![]() 的图像在x轴上截得的线段长的取值范围.
的图像在x轴上截得的线段长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com