
【题目】对于双曲线![]() ,定义
,定义![]() 为其伴随曲线,记双曲线
为其伴随曲线,记双曲线![]() 的左、右顶点为
的左、右顶点为![]() 、
、![]() .
.
(1)当![]() 时,记双曲线
时,记双曲线![]() 的半焦距为
的半焦距为![]() ,其伴随椭圆
,其伴随椭圆![]() 的半焦距为
的半焦距为![]() ,若
,若![]() ,求双曲线
,求双曲线![]() 的渐近线方程.
的渐近线方程.
(2)若双曲线![]() 的方程为
的方程为![]() ,弦
,弦![]() 轴,记直线
轴,记直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求其动点
,求其动点![]() 的轨迹方程.
的轨迹方程.
(3)过双曲线![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,求证:对任意的
两点,求证:对任意的![]() ,在伴随曲线
,在伴随曲线![]() 上总存在点
上总存在点![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)利用双曲线的![]() 、
、![]() 、
、![]() 的关系及椭圆的
的关系及椭圆的![]() 、
、![]() 、
、![]() 的关系及双曲线的渐近线的方程即可得出;(2)设出点
的关系及双曲线的渐近线的方程即可得出;(2)设出点![]() 、
、![]() 的坐标,利用点斜式得出直线
的坐标,利用点斜式得出直线![]() 、
、![]() 的方程,联立即可得出交点
的方程,联立即可得出交点![]() 的坐标,反解出点
的坐标,反解出点![]() 的坐标,利用代点法即可求出轨迹;(3)设出直线
的坐标,利用代点法即可求出轨迹;(3)设出直线![]() 的方程,并与双曲线的方程联立,利用根与系数的关系及已知条件求出
的方程,并与双曲线的方程联立,利用根与系数的关系及已知条件求出![]() 的范围,再求出伴随曲线
的范围,再求出伴随曲线![]() 上的任意一点到点
上的任意一点到点![]() 的距离的平方的取值范围,即可判断出结论是否成立.
的距离的平方的取值范围,即可判断出结论是否成立.
(1)∵![]() ,
,![]() ,由
,由![]() ,
,
得![]() ,即
,即![]()
可得![]() ,
,
∴![]() 的渐近线方程为
的渐近线方程为![]() ;
;
(2)设![]() ,
,![]() ,
,
又![]() 、
、![]() ,
,
∴直线![]() 的方程为
的方程为![]() …①
…①
直线![]() 的方程为
的方程为![]() …②,
…②,
由①②得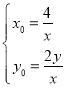 ,
,
∵![]() 在双曲线
在双曲线![]() 上,
上,
∴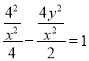 ,整理得
,整理得![]() .
.
(3)证明:点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
设![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
则由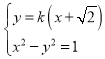 得
得![]() ,
,
即![]() ,
,
当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]()
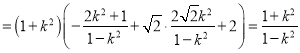 ,
,
由![]() 知
知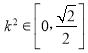 ,
,
∴![]() .
.
∵双曲线![]() 的伴随曲线是圆
的伴随曲线是圆![]() ,
,
圆![]() 上任意一点
上任意一点![]() 到
到![]() 的距离
的距离![]() ,
,
∴![]() ,
,
∵![]()
∴对任意的![]() ,在伴随曲线
,在伴随曲线![]() 上总存在点
上总存在点![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列性质的函数![]() 的全体;在定义域内存在实数t,使得
的全体;在定义域内存在实数t,使得![]() .
.
(1)判断![]() 是否属于集合M,并说明理由;
是否属于集合M,并说明理由;
(2)若![]() 属于集合M,求实数a的取值范围;
属于集合M,求实数a的取值范围;
(3)若![]() ,求证:对任意实数b,都有
,求证:对任意实数b,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),其准线方程
),其准线方程![]() ,直线
,直线![]() 过点
过点![]() (
(![]() ),且与抛物线交于
),且与抛物线交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求抛物线方程,并注明:![]() 的值与直线
的值与直线![]() 倾斜角的大小无关;
倾斜角的大小无关;
(2)若![]() 为抛物线上的动点,记
为抛物线上的动点,记![]() 的最小值为函数
的最小值为函数![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为给定的不小于
为给定的不小于![]() 的正整数,考察
的正整数,考察![]() 个不同的正整数
个不同的正整数![]() ,
,![]() ,
,![]() ,
,![]() 构成的集合
构成的集合![]() ,若集合
,若集合![]() 的任何两个不同的非空子集所含元素的总和均不相等,则称集合
的任何两个不同的非空子集所含元素的总和均不相等,则称集合![]() 为“差异集合”.
为“差异集合”.
(1)分别判断集合![]() ,集合
,集合![]() 是否是“差异集合”;(只需写出结论)
是否是“差异集合”;(只需写出结论)
(2)设集合![]() 是“差异集合”,记
是“差异集合”,记![]() ,求证:数列
,求证:数列![]() 的前
的前![]() 项和
项和![]()
![]() ;
;
(3)设集合![]() 是“差异集合”,求
是“差异集合”,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
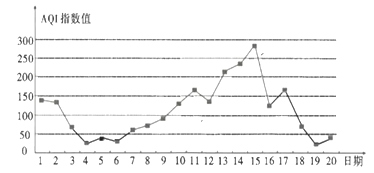
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老年人120人,中年人360人,青年人n人,为调查身体健康状况,需要从中抽取一个容量为m的样本,用分层抽样的方法进行抽样调查,样本中的中年人为6人,则n和m的值不可以是下列四个选项中的哪组( )
A.n=360,m=14B.n=420,m=15C.n=540,m=18D.n=660,m=19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元),这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据![]() (单位:十亿元).绘制如下表1:
(单位:十亿元).绘制如下表1:
表1
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额 | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示.
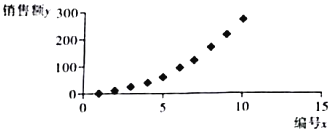
把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为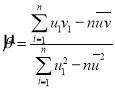 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com