
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向
向
圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.

(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
(3)试问![]() 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由圆![]() 的方程可知,圆
的方程可知,圆![]() 的半径
的半径![]() ,
,![]() ,由此可求出圆的方程;(2)由已知得直线
,由此可求出圆的方程;(2)由已知得直线![]() 和
和![]() 都与圆
都与圆![]() 相切,化简可得
相切,化简可得![]() ,再利用点在椭圆上,即可求解
,再利用点在椭圆上,即可求解![]() 的值;(3)当直线
的值;(3)当直线![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,利用直线方程与椭圆的方程联立方程组,得出
,利用直线方程与椭圆的方程联立方程组,得出![]() ,同理
,同理![]() ,由此可求解
,由此可求解![]() 为定值.
为定值.
试题解析:(1)由圆![]() 的方程知圆
的方程知圆![]() 的半径
的半径![]() ,因为直线
,因为直线![]() ,
,![]() 互相垂直,且和圆
互相垂直,且和圆![]() 相切,所以
相切,所以![]() ,即
,即![]() ①
①
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ②
②
联立①②,解得 ,所以,所求圆
,所以,所求圆![]() 的方程为
的方程为![]() .
.
(2)因为直线![]()
![]() 和
和![]()
![]() 都与圆
都与圆![]() 相切,所以
相切,所以 ,
, ,化简得
,化简得![]() ,因为点
,因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,即
,即![]() ,所以
,所以 .
.
(3)方法一(1)当直线![]() ,
,![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,
,![]() ,
,
由(2)知![]() ,所以
,所以![]() ,故
,故![]() .因为
.因为![]() ,
,![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,所以
,所以![]() ,
,
整理得![]() ,所以
,所以![]()
所以![]() .
.
方法(二)(1)当直线![]() ,
,![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,
,![]() ,
,
联立 ,解得
,解得![]() ,
,![]() ,所以
,所以 ,
,
同理,得 .由(2)
.由(2)![]() ,得
,得![]() ,
,
所以
 .
.
(2)当直线![]() ,
,![]() 落在坐标轴上时,显然有
落在坐标轴上时,显然有![]() .
.
综上:![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】如图甲是某商店2018年(按360天计算)的日盈利额(单位:万元)的统计图.
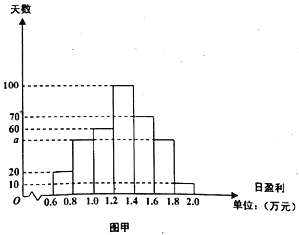
(1)请计算出该商店2018年日盈利额的平均值(精确到0.1,单位:万元):
(2)为了刺激消费者,该商店于2019年1月举行有奖促销活动,顾客凡购买一定金额的高品后均可参加抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店对前5天抽奖活动的人数进行统计如下表:(![]() 表示第
表示第![]() 天参加抽奖活动的人数)
天参加抽奖活动的人数)
| 1 | 2 | 3 | 4 | 5 |
| 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(ⅰ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() :
:
(ⅱ)该商店采取转盘方式进行抽奖(如图乙),其中转盘是个八等分的圆.每位顾客最多两次抽奖机会,若第一次抽到奖,则抽奖终止,若第一次未抽到奖,则再提供一次抽奖机会.抽到一等奖的奖品价值128元,抽到二等奖的奖品价值32元.若该商店此次抽奖活动持续7天,试估计该商店在此次抽奖活动结束时共送出价值为多少元的奖品(精确到0.1,单位:万元)?
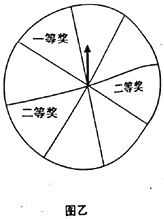
(3)用(1)中的2018年日盈利额的平均值去估计当月(共31天)每天的日盈利额.若商店每天的固定支出约为1000元,促销活动日的日盈利额比平常增加20%,则该商店当月的纯利润约为多少万元?(精确到0.1,纯利润=盈利额-固定支出-抽奖总奖金数)
参考公式及数据: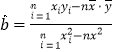 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数 ![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏, 从中部选择河北. 湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以频率作为概率, 某普查小组从该小区随机选择 1 家企事业单位,3 家个体经营户作为普查对象,入户登记顺利的对象数记为![]() , 写出
, 写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.88 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上(不包括端点).
上(不包括端点).

(1)求证:![]()
(2)是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com