
【题目】已知![]() ,
,![]() .
.
(1)若直线![]() 与圆
与圆![]() :
:![]() 相切,求
相切,求![]() 被圆
被圆![]() :
:![]() 所截得弦长取最小值时直线
所截得弦长取最小值时直线![]() 的斜率;
的斜率;
(2)![]() 时,
时,![]() :
:![]() 表示圆,问是否存在一条直线
表示圆,问是否存在一条直线![]() ,使得它和所有的圆
,使得它和所有的圆![]() 都没有公共点?如果存在,求出直线
都没有公共点?如果存在,求出直线![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)若满足不等式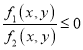 和等式
和等式![]() 的点集是一条线段,求
的点集是一条线段,求![]() 取值范围.
取值范围.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() :
:![]() ;(3)
;(3)![]() .
.
【解析】
(1)画出图像分析可得, 直线![]() 与直线
与直线![]() 垂直时
垂直时![]() 被圆
被圆![]() :
:![]() 所截得弦长取最小值.
所截得弦长取最小值.
再根据垂直的直线斜率之积为-1求解即可.
(2)当![]() 时代入
时代入![]() 有
有
![]() ,即
,即![]() 又
又![]() ,故猜测存在一条直线
,故猜测存在一条直线![]() ,使得它和所有的圆
,使得它和所有的圆![]() 都没有公共点,再证明即可.
都没有公共点,再证明即可.
(3) ![]() 的解集为
的解集为![]() 或
或![]() 两条直线,
两条直线, 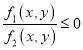 为两圆之间的部分,数形结合列式求解即可.
为两圆之间的部分,数形结合列式求解即可.
(1)由![]() ,
,
即![]() 圆心
圆心![]() ,半径
,半径![]()
![]()
即![]() 圆心
圆心![]() ,半径
,半径![]()
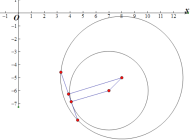
因为当![]() 被圆
被圆![]() :
:![]() 所截得弦长取最小值时,圆心
所截得弦长取最小值时,圆心![]() 到直线
到直线![]() 的距离最大.
的距离最大.
又![]() 到
到![]() 的距离
的距离![]() ,当且仅当直线
,当且仅当直线![]() 与直线
与直线![]() 垂直时取得
垂直时取得![]() 为最大值,此时
为最大值,此时![]() 斜率
斜率![]() ,故直线
,故直线![]() 斜率
斜率![]()
(2) 存在,![]() :
:![]() 和所有的圆
和所有的圆![]() 都没有公共点.
都没有公共点.
证明:由题![]() :
:![]() ,
,![]() 即
即
![]() ,
,
变形得![]()
即![]() ,
,
故![]() :
:![]()
若![]() 与
与![]() 有交点,则
有交点,则
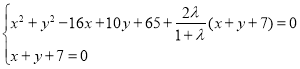 有解.上式减去
有解.上式减去![]() 倍的下式有:
倍的下式有:
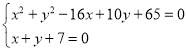 有解.
有解.
即圆![]() 与直线
与直线![]() 有交点,圆半径
有交点,圆半径![]()
但圆心![]() 到
到![]() 距离
距离![]() .
.
故圆![]() 与直线
与直线![]() 无交点.
无交点.
即![]() 和所有的圆
和所有的圆![]() 都没有公共点.
都没有公共点.
(3)由题得![]() 的解集为
的解集为![]() 或
或![]() 两条直线,
两条直线,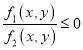 得
得![]() 且
且![]()
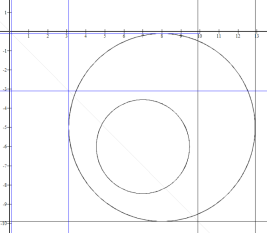
即为两圆![]()
![]() 与
与![]()
![]() 之间的部分.
之间的部分.
又若不等式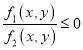 和等式
和等式![]() 的点集是一条线段,则需注意临界条件.
的点集是一条线段,则需注意临界条件.
当![]() 与圆
与圆![]() 相切时,
相切时,![]() 或
或![]() ,
,
当![]() 与圆
与圆![]() 相切时,
相切时,![]() 或
或![]()
又因为![]() 到所求的所有
到所求的所有![]() 的距离都大于半径
的距离都大于半径![]() ,故无需考虑圆
,故无需考虑圆![]() 对形成线段的影响.
对形成线段的影响.
故![]()


科目:高中数学 来源: 题型:
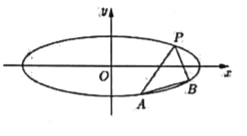
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
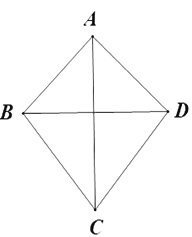
【题目】如图,欲在一四边形花坛![]() 内挖一个等腰三角形的水池
内挖一个等腰三角形的水池![]() ,且
,且![]() ,已知四边形
,已知四边形![]() 中,
中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() 米,
米,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() 的大小为
的大小为![]() ,要求
,要求![]() 的三个顶点在花坛的边缘上(即在四边形
的三个顶点在花坛的边缘上(即在四边形![]() 的边上),设点
的边上),设点![]() 到水池底边
到水池底边![]() 的距离为
的距离为![]() ,水池的面积为
,水池的面积为![]() 平方米.
平方米.
(1)求![]() 的长;
的长;
(2)试将![]() 表示成关于
表示成关于![]() 的函数,并求出
的函数,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]()
(1)若函数f(x)有两个零点,求实数a的取值范围;
(2)若a=3,且对任意的x1∈[-1,2],总存在![]() ,使g(x1)-f(x2)=0成立,求实数m的取值范围.
,使g(x1)-f(x2)=0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂产生的废气经过过滤后排放,在过滤过程中,污染物的数量p(单位:毫克/升)不断减少,已知p与时间t(单位:小时)满足p(t)=![]() ,其中p0为t=0时的污染物数量.又测得当t∈[0,30]时,污染物数量的变化率是-10ln 2,则p(60)=( )
,其中p0为t=0时的污染物数量.又测得当t∈[0,30]时,污染物数量的变化率是-10ln 2,则p(60)=( )
A.150毫克/升B.300毫克/升
C.150ln 2毫克/升D.300ln 2毫克/升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 是函数
是函数![]() 的一个极值点,试求
的一个极值点,试求![]() 的单调区间;
的单调区间;
(2)若![]() 且
且![]() ,是否存在实数a,使得
,是否存在实数a,使得![]() 在区间
在区间![]() 上的最大值为4?若存在,求出实数a的值;若不存在,请说明理由.
上的最大值为4?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
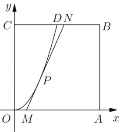
【题目】某地要建造一个边长为2(单位:![]() )的正方形市民休闲公园
)的正方形市民休闲公园![]() ,将其中的区域
,将其中的区域![]() 开挖成一个池塘,如图建立平面直角坐标系后,点
开挖成一个池塘,如图建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 是函数
是函数![]() 图像的一部分,过边
图像的一部分,过边![]() 上一点
上一点![]() 在区域
在区域![]() 内作一次函数
内作一次函数![]() (
(![]() )的图像,与线段
)的图像,与线段![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 重合),且线段
重合),且线段![]() 与曲线
与曲线![]() 有且只有一个公共点
有且只有一个公共点![]() ,四边形
,四边形![]() 为绿化风景区.
为绿化风景区.
(1)求证:![]() ;
;
(2)设点![]() 的横坐标为
的横坐标为![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 两点的坐标;
两点的坐标;
②将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且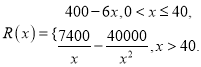
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com