
【题目】双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点,直线
有相同的焦点,直线![]() 为双曲线
为双曲线![]() 的一条渐近线.
的一条渐近线.
(1)求双曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点(
点(![]() 点与
点与![]() 的顶点不重合),当
的顶点不重合),当![]() ,且
,且![]() ,求
,求![]() 点的坐标.
点的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据双曲线的焦点、渐近线方程、结合![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() 的值,进而求得双曲线方程.
的值,进而求得双曲线方程.
(2)设出直线![]() 的方程和
的方程和![]() 两点的坐标,求得
两点的坐标,求得![]() 点坐标,利用
点坐标,利用![]() 和
和![]() ,结合向量共线的坐标运算,求得
,结合向量共线的坐标运算,求得![]() ①,通过联立直线方程和双曲线方程,写出韦达定理并代入①,由此求得直线的斜率,进而求得
①,通过联立直线方程和双曲线方程,写出韦达定理并代入①,由此求得直线的斜率,进而求得![]() 点坐标.
点坐标.
(1)依题意可知:椭圆![]() 焦点坐标为
焦点坐标为![]() ,故双曲线
,故双曲线![]() 的半焦距为
的半焦距为![]() .由于双曲线的渐近线为
.由于双曲线的渐近线为![]() ,故
,故![]() ,结合
,结合![]() 可解得
可解得![]() .故双曲线方程为
.故双曲线方程为![]() .
.
(2)由题意知直线![]() 的斜率
的斜率![]() 存在且不等于零,设直线
存在且不等于零,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以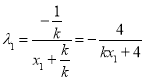 ,同理
,同理![]() ,所以
,所以![]() ,即
,即![]() ①,又
①,又![]() 以及
以及![]() ,消去
,消去![]() 得
得![]() .当
.当![]() 时,直线
时,直线![]() 与双曲线的渐近线平行,不合题意,所以
与双曲线的渐近线平行,不合题意,所以![]() .由韦达定理有
.由韦达定理有![]() ,代入①得
,代入①得![]() ,
,![]() ,所以所求
,所以所求![]() 点的坐标为
点的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】我们在求高次方程或超越方程的近似解时常用二分法求解,在实际生活中还有三分法.比如借助天平鉴别假币.有三枚形状大小完全相同的硬币,其中有一假币(质量较轻),把两枚硬币放在天平的两端,若天平平衡,则剩余一枚为假币,若天平不平衡,较轻的一端放的硬币为假币.现有 27 枚这样的硬币,其中有一枚是假币(质量较轻),如果只有一台天平,则一定能找到这枚假币所需要使用天平的最少次数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-![]() x3+2x2+2x,若存在满足0≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
x3+2x2+2x,若存在满足0≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
A. [6,+∞)B. (-∞,2]
C. [2,6]D. [5,6]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点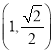 ,若点
,若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭点”.
称为点M的一个“椭点”.
(1)求椭圆C的标准方程;
(2)若直线![]() 与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试判断
与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试判断![]() 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是
是![]() 的两个非空子集,如果存在一个函数
的两个非空子集,如果存在一个函数![]() 满足:①
满足:① ![]() ;② 对任意
;② 对任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,那么称这两个集合为“
,那么称这两个集合为“![]() 到
到![]() 的保序同构”,以下集合对不是“
的保序同构”,以下集合对不是“![]() 到
到![]() 的保序同构”的是( )
的保序同构”的是( )
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com