已知圆C经过点A(0,3)和B(3,2),且圆心C在直线y=x上.
(Ⅰ) 求圆C的方程;
(Ⅱ)若直线y=2x+m被圆C所截得的弦长为4,求实数m的值.
【答案】
分析:(Ⅰ)设圆C的圆心坐标为C(a,a),再由圆C经过A(0,3)、B(3,2)两点,可得|CA|
2=|CB|
2,即可求得圆心坐标和半径,从而求得圆C的方程.
(Ⅱ)通过圆心距、半径、半弦长满足的勾股定理,即可求实数m的值.
解答:解:(Ⅰ)由于圆心在直线y=x上,故可设圆C的圆心坐标为C(a,a). 再由圆C经过A(0,3)、B(3,2)两点,
可得|CA|=|CB|,∴|CA|
2=|CB|
2,∴(a-0)
2+(a-3)
2=(a-3)
2+(a-2)
2.
解得 a=1,故圆心C(1,1),半径r=
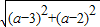
=
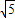
,
故圆C的方程为 (x-1)
2+(y-1)
2=5,
(Ⅱ)圆心C(1,1),半径r=
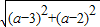
=
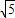
,
圆心到直线y=2x+m的距离为:
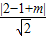
=
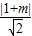
直线被圆C所截得的弦长为4,所以半弦长为:2;
所以(
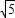
)
2=2
2+(
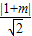
)
2,
所以实数m的值为-1
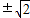
.
点评:本题主要考查求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键,属于中档题.

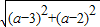 =
=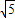 ,
,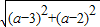 =
=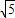 ,
,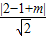 =
=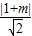
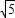 )2=22+(
)2=22+(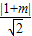 )2,
)2,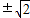 .
.

 阅读快车系列答案
阅读快车系列答案