
【题目】一个盒子中装有4个编号依次为1、2、3、4的球,这4个球除号码外完全相同,先从盒子中随机取一个球,该球的编号为X,将球放回袋中,然后再从袋中随机取一个球,该球的编号为Y
(1)列出所有可能结果.
(2)求事件A=“取出球的号码之和小于4”的概率.
(3)求事件B=“编号X<Y”的概率.
【答案】
(1)解:所有可能的结果共有(1,1)、(1,2)、(1,3)、(1,4)、(2,1)、(2,2)、(2,3)、(2,4)、
(3,1)、(3,2)、(3,3)、(3,4)、(4,1)、(4,2)、(4,3)、(4,4),共计16个
(2)解:事件“取出球的号码之和小于4”包含的结果有(1,1)、(1,2)、(2,1),共计3个,
故“取出球的号码之和小于4”的概率为 ![]()
(3)解:事件B=“编号X<Y”包含的结果有 (1,2)、(1,3)、(1,4)、(2,3)、(2,4)、(3,4),共计6个,
故事件B=“编号X<Y”的概率为 ![]() =
= ![]()
【解析】(1)用列举法求得所有可能的结果共有 16个.(2)用列举法求得事件“取出球的号码之和小于4”包含的结果有3个,由此求得“取出球的号码之和小于4”的概率.(3)用列举法求得事件B=“编号X<Y”包含的结果有 6个,由此求得事件B=“编号X<Y”的概率.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx+![]() ax2+x+1.
ax2+x+1.
(I)a=﹣2时,求函数f(x)的极值点;
(Ⅱ)当a=0时,证明xex≥f(x)在(0,+∞)上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
分组 | 频数 | 频率 |
[0,1) | 10 | b |
[1,2) | 20 | 0.20 |
[2,3) | a | 0.30 |
[3,4) | 20 | 0.20 |
[4,5) | 10 | 0.10 |
[5,6] | 10 | 0.10 |
合计 | 100 | 1.00 |
(1)求表中a和b的值;
(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从盛满2升纯酒精的容器里倒出1升,然后加满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒次后才能使纯酒精体积与总溶液的体积之比低于10%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
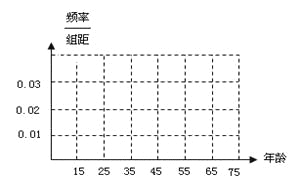
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
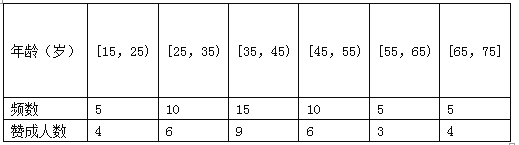
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2eax , a>0.
(1)证明:函数y=f(x)在(0,+∞)上为增函数;
(2)若方程f(x)﹣1=0有且只有两个不同的实数根,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com