
����Ŀ����ij��ҵ������ij�ֲ�Ʒ�г�ȡ100����������Щ��Ʒ��һ������ָ��ֵ���ɲ������������Ƶ���ֲ�����
����ָ��ֵ���� | [75��85�� | [85��95�� | [95��105�� | [105��115�� | [115��125�� |
Ƶ�� | 6 | 26 | 38 | 22 | 8 |

��1��������Щ���ݵ�Ƶ���ֲ�ֱ��ͼ��
��2���������ֲ�Ʒ����ָ��ֵ��ƽ���������ͬһ���е������ø���������м�ֵ���������ֲ�Ʒ������ָ��ֵ����
��3���������ϳ����������ݣ��ܷ���Ϊ����ҵ���������ֲ�Ʒ���ϡ�����ָ��ֵ������95�IJ�Ʒ����Ҫռȫ����Ʒ��85%���Ĺ涨��
���𰸡�
��1���⣺����֪����Ƶ�ʷֲ���Ϊ��
����ָ��ֵ���� | [75��85�� | [85��95�� | [95��105�� | [105��115�� | [115��125�� |
Ƶ�� | 6 | 26 | 38 | 22 | 8 |
Ƶ�� | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
��Ƶ�ʷֲ���������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼΪ

��2���⣺����ָ��ֵ������ƽ����Ϊ ![]() =
= ![]() =100��
=100��
����ָ��ֵ����������Ϊs2=����20��2��0.06+����10��2��0.26+0��0.38+102��0.22+202��0.08=104��
�����ֲ�Ʒ����ָ���ƽ��������ֵΪ100������Ĺ���ֵΪ104
��3���⣺������ ![]() =68%��80%��
=68%��80%��
�����ҵ���������ֲ�Ʒ�����ϡ�����ָ��ֵ������95�IJ�Ʒ����Ҫռȫ����Ʒ��80%���Ĺ涨
����������1������֪����Ƶ�ʷֲ������ɴ�������������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ����2����Ƶ�ʷֲ�ֱ��ͼ���������ָ��ֵ������ƽ�����������3������ָ��ֵ������95�IJ�Ʒ��ռ�����Ĺ���ֵ�����ڸù���ֵС��0.8���ʲ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ������95 �IJ�Ʒ����Ҫռȫ����Ʒ80%�Ĺ涨��
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ�ǽ����ĸ�������Ҫ֪��Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC��A1B1C1���е��ⳤ��Ϊ2��A1B= ![]() ��A1B��AC��
��A1B��AC�� 
������֤��A1C1��B1C��
������ֱ��AC��ƽ��ABB1A1���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin����x+�գ����أ�0����
sin����x+�գ����أ�0���� ![]() ���գ�
���գ� ![]() ����A��
����A�� ![]() ��0��Ϊf��x��ͼ��ĶԳ����ģ�B��C�Ǹ�ͼ�������ڵ���ߵ����͵㣬��BC=4����f��x���ĵ������������ǣ� ��
��0��Ϊf��x��ͼ��ĶԳ����ģ�B��C�Ǹ�ͼ�������ڵ���ߵ����͵㣬��BC=4����f��x���ĵ������������ǣ� ��
A.��2k�� ![]() ��2k+
��2k+ ![]() ����k��Z
����k��Z
B.��2k�� ![]() ��2k��+
��2k��+ ![]() ����k��Z
����k��Z
C.��4k�� ![]() ��4k+
��4k+ ![]() ����k��Z
����k��Z
D.��4k�� ![]() ��4k��+
��4k��+ ![]() ����k��Z
����k��Z
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�У�a2=2����ǰn���Sn���㣺 ![]() ��n��N*����
��n��N*����
����������{an}��ͨ�ʽ��
������ ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������a��3��5��7��ƽ������b����a��b�ֱ�������{2n��2}��n��N*���ĵ�2��͵�4�����������ķ����ǣ� ��
A.3
B.4
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=eax��a��0����
��1���� ![]() ʱ����
ʱ���� ![]() ��x��0��������g��x����[m��m+1]��m��0���ϵ���Сֵ��
��x��0��������g��x����[m��m+1]��m��0���ϵ���Сֵ��
��2��������һ��x��R��f��x����x��1��0���������a��ȡֵ���ϣ�
��3����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������������������࣬������ȾΣ�����أ�������Ⱦ�������ļ¡��������ѵ��ķμ�����Ϊ�˽�ij���ķμ����Ƿ����Ա��йأ���ijҽԺ����Ķ���Ժ50�˽������ʾ�����õ������µ���������
���ķμ��� | �����ķμ��� | �ϼ� | |
�� | 5 | ||
Ů | 10 | ||
�ϼ� | 50 |
��֪��ȫ��50���������ȡ1�ˣ��鵽���ķμ������˵ĸ���Ϊ ![]() ��
��
�����뽫���������������������
�����Ƿ���99.5%�İ�����Ϊ���ķμ������Ա��йأ�˵��������ɣ�
������֪�ڻ��ķμ�����10λŮ���У���3λ�ֻ�θ�������ڴӻ��ķμ�����10λŮ���У�ѡ��3����������������Ų飬��ѡ����θ����Ů������Ϊ�Σ���εķֲ��У���ѧ�����Լ����������Ⱦ��������ּ�������dz̸�ճ���������μ��ٴ�����Ⱦ��
������ٽ�ֵ�����ο���
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽK2= ![]() ����n=a+b+c+d��
����n=a+b+c+d��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC��A1B1C1�У�����AA1�͵���A1B1C1 �� AA1=AC=BC=1����ACB=90�㣬D��A1B1���е㣬F��BB1�ϵĵ㣬AB1 �� DF���ڵ�E����AB1��DF�������н����в���ȷ���ǣ� �� 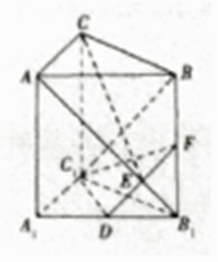
A.CE��BC1�����Ҵ�ֱ
B.AB1��C1F
C.��C1DF��ֱ��������
D.DF�ij�Ϊ ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com