
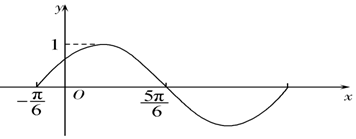
分析 根据函数的图象求出f(x)的解析式,几次考察各项可得答案.
解答 解:由图象可知A=1,T=2×$(\frac{5π}{6}+\frac{π}{6})$=2π,
∵T=$\frac{2π}{ω}=2π$,
∴ω=1
可得f(x)=sin(x+φ)
图象过点($-\frac{π}{6}$,0),故sin($-\frac{π}{6}$+φ)=0,
解得:φ=$\frac{π}{6}$.
∴函数f(x)=sin(x+$\frac{π}{6}$),∴②对
由对称中心:x+$\frac{π}{6}$=kπ,可得x=k$π-\frac{π}{6}$,函数f(x)的对称中心是(-$\frac{π}{6}$+kπ,0)(k∈Z),∴①不对
x∈[0,$\frac{π}{2}$]上,则x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],当x+$\frac{π}{6}$=$\frac{π}{6}$时,f(x)取得最小值为$\frac{1}{2}$,∴③对.
把函数f(x)图象上每一点的横坐标缩短为原来的$\frac{1}{3}$倍,可得g(x)=sin(3x+$\frac{π}{6}$),图象没有关于y轴对称,∴④不对.故②③对.
故答案为:②③
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=x+1 | B. | $\widehat{y}$=x+2 | C. | $\widehat{y}$=2x+1 | D. | $\widehat{y}$=x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | F一定是奇数,G可能是奇数 | B. | F可能是偶数,G一定是偶数 | ||
| C. | F一定是奇数,G一定是偶数 | D. | F可能是偶数,G可能是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com