
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ),在同一个周期内,当
),在同一个周期内,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,当
,当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
(1)求函数![]() 的解析式,并求
的解析式,并求![]() 在[0,
在[0,![]() ]上的单调递增区间.
]上的单调递增区间.
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,方程
的图象,方程![]() 在
在![]() 有2个不同的实数解,求实数a的取值范围.
有2个不同的实数解,求实数a的取值范围.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】万众瞩目的2018年俄罗斯世界杯决赛于北京时间2018年7月15日23时在俄罗斯莫斯科的卢日尼基体育场进行.为确保总决赛的顺利进行,组委会决定在比赛地点卢日尼基球场外临时围建一个矩形观众候场区,总面积为![]() (如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为
(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为![]() 的入口.现已知铁栏杆的租用费用为100元/
的入口.现已知铁栏杆的租用费用为100元/![]() .设该矩形区域的长为
.设该矩形区域的长为![]() (单位:
(单位:![]() ),租用铁栏杆的总费用为
),租用铁栏杆的总费用为![]() (单位:元).
(单位:元).

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机械厂欲从![]() 米,
米,![]() 米的矩形铁皮中裁剪出一个四边形
米的矩形铁皮中裁剪出一个四边形![]() 加工成某仪器的零件,裁剪要求如下:点
加工成某仪器的零件,裁剪要求如下:点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
,![]() .设
.设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (单位:平方米).
(单位:平方米).

(1)求![]() 关于
关于![]() 的函数关系式,求出定义域;
的函数关系式,求出定义域;
(2)当![]() 的长为何值时,裁剪出的四边形
的长为何值时,裁剪出的四边形![]() 的面积最小,并求出最小值.
的面积最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,其对称轴在
,其对称轴在![]() 轴右侧,有下列结论:①抛物线经过点
轴右侧,有下列结论:①抛物线经过点![]() ;②方程
;②方程![]() 有两个不相等的实数根;③
有两个不相等的实数根;③![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(1)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(3)无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积的经验公式为:![]() .弧田(如图1阴影部分)由圆弧和其所对弦围成,弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式:
.弧田(如图1阴影部分)由圆弧和其所对弦围成,弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式:![]() 圆面积
圆面积![]() 矢
矢![]() .球缺是指一个球被平面截下的一部分,厦门嘉庚体育馆近似球缺结构(如图3),若该体育馆占地面积约为18000
.球缺是指一个球被平面截下的一部分,厦门嘉庚体育馆近似球缺结构(如图3),若该体育馆占地面积约为18000![]() ,建筑容积约为340000
,建筑容积约为340000![]() ,估计体育馆建筑高度(单位:
,估计体育馆建筑高度(单位:![]() )所在区间为( )
)所在区间为( )
参考数据: ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.



A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+2xtanθ-1,x∈[-1,![]() ],其中θ∈(-
],其中θ∈(-![]() ,
,![]() ).
).
(1)当θ=-![]() 时,求函数f(x)的最大值;
时,求函数f(x)的最大值;
(2)求θ的取值范围,使y=f(x)在区间[-1,![]() ]上是单调函数.
]上是单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
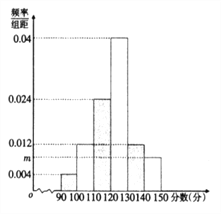
(1)求![]() 的值及这50名同学数学成绩的平均数
的值及这50名同学数学成绩的平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,若已知成在
的同学中选出3位作为代表进行座谈,若已知成在![]() 的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com