
【题目】已知函数f(x)= ![]() (x≠1)
(x≠1)
(1)证明f(x)在(1,+∞)上是减函数;
(2)令g(x)=lnf(x),判断g(x)=lnf(x)的奇偶性并加以证明.
【答案】
(1)证明: ![]() ,设x1>x2>1,则:
,设x1>x2>1,则:
![]()
= ![]() ;
;
∵x1>x2>1;
∴x2﹣x1<0,x1﹣1>0,x2﹣1>0;
∴ ![]() ;
;
∴f(x1)<f(x2);
∴f(x)在(1,+∞)上是减函数
(2)解: ![]() ;
;
∴ ![]() ;
;
解 ![]() 得,x<﹣1,或x>1;
得,x<﹣1,或x>1;
![]() ;
;
∴g(x)为奇函数
【解析】(1)分离常数得到 ![]() ,根据减函数的定义,设任意的x1>x2>1,然后作差,通分,证明f(x1)<f(x2)即得出f(x)在(1,+∞)上是减函数;(2)先求出
,根据减函数的定义,设任意的x1>x2>1,然后作差,通分,证明f(x1)<f(x2)即得出f(x)在(1,+∞)上是减函数;(2)先求出 ![]() ,然后求g(x)的定义域,并根据对数的运算求出g(﹣x)=﹣g(x),这样便得出g(x)为奇函数.
,然后求g(x)的定义域,并根据对数的运算求出g(﹣x)=﹣g(x),这样便得出g(x)为奇函数.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较),还要掌握函数的奇偶性(偶函数的图象关于y轴对称;奇函数的图象关于原点对称)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ax2﹣3x.
(1)若a=4时,求f(x)在x∈[1,4]上的最大值和最小值;
(2)若f(x)在x∈[2,+∞]上是增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
参考公式: 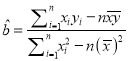 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若a=2,b= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,椭圆C上任意一点到椭圆左右两个焦点的距离之和为4.
(a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,椭圆C上任意一点到椭圆左右两个焦点的距离之和为4.
(1)求椭圆C的方程;
(2)椭圆C与X轴负半轴交于点A,直线过定点(﹣1,0)交椭圆于M,N两点,求△AMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数y= ![]() +
+ ![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;
③f(x)是定义在R上的奇函数,当x<0时,f(x)=2x2+x﹣1,则x≥0时,f(x)=﹣2x2+x+1
④函数y= ![]() 的值域是(﹣1,
的值域是(﹣1, ![]() ).
).
其中正确命题的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为正方形,
为正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
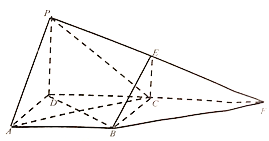
(1)若![]() 和
和![]() 延长交于点
延长交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 边上的动点,求直线
边上的动点,求直线![]() 与平面
与平面![]() 所成角正弦值的最小值.
所成角正弦值的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com