
【题目】在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有3个红球和7个白球,这些球除颜色外完全相同,一次从中摸出3个球.
(1)设![]() 表示摸出的红球的个数,求
表示摸出的红球的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)为了提高同学们参与游戏的积极性,参加游戏的同学每人可摸球两次,每次摸球后放回,若规定两次共摸出红球的个数不少于![]() ,且中奖概率大于60%时,即中奖,求
,且中奖概率大于60%时,即中奖,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】设直线l的方程为![]() ,圆O的方程为
,圆O的方程为![]() .
.
(1)当m取一切实数时,直线l与圆O都有公共点,求r的取值范围;
(2)当![]() 时,直线
时,直线![]() 与圆O交于M,N两点,若
与圆O交于M,N两点,若![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住2022年冬奥会契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和销售策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.
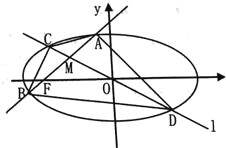
(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为k的直线l经过抛物线y=![]() x2的焦点F,且与抛物线相交于A,B两点,若线段|AB|的长为8.
x2的焦点F,且与抛物线相交于A,B两点,若线段|AB|的长为8.
(1)求抛物线的焦点F的坐标和准线方程;
(2)求直线的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在(0,+
在(0,+![]() )上恒成立,求实数
)上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】屠呦呦,第一位获得诺贝尔科学奖项的中国本土科学家,在2015年获得诺贝尔生理学或医学奖,理由是她发现了青蒿素.这种药品可以有效降低疟疾患者的死亡率,从青篙中提取的青篙素抗疟性超强,几乎达到100%.据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
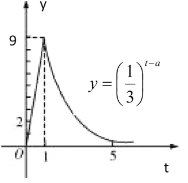
(Ⅰ)写出服药一次后y与t之间的函数关系式![]() ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,平行于
中,平行于![]() 轴且过点
轴且过点![]() 的入射光线
的入射光线![]() 被直线
被直线![]() 反射,反射光线
反射,反射光线![]() 交
交![]() 轴于
轴于![]() 点,圆
点,圆![]() 过点
过点![]() ,且与
,且与![]() 、
、![]() 相切.
相切.
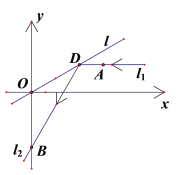
(Ⅰ)求![]() 所在直线的方程;
所在直线的方程;
(Ⅱ)求圆![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com