
分析 (Ⅰ)利用诱导公式化解即可得f(α);
(Ⅱ)根据同角三角函数关系式,可求f(α)的值.
解答 解:(Ⅰ)$f(α)=\frac{{sin({\frac{π}{2}-α})sin({-α})tan({π-α})}}{{tan({-α})sin({π-α})}}$=$\frac{{cosα({-sinα})({-tanα})}}{{({-tanα})sinα}}=-cosα$.
(Ⅱ)由$cos({\frac{3}{2}π-α})=\frac{2}{3}$,得$sinα=-\frac{2}{3}$.
又∵α为第四象限角,
∴$cosα=\sqrt{1-{{sin}^2}α}=\frac{{\sqrt{5}}}{3}$.
故得$f(α)=-\frac{{\sqrt{5}}}{3}$.
点评 本题考查了诱导公式的化简能力和同角三角函数关系式的运用,属于基础题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}e$ | C. | e | D. | 2e |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
已知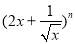 的展开式前两项的二项式系数之和为10.
的展开式前两项的二项式系数之和为10.
(1)求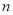 的值.
的值.
(2)求出这个展开式中的常数项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com