已知函数f(x)对任意的m,n∈R,都有f(m+n)=f(m)+f(n),并且x>0时恒有f(x)>0
(1)求证:f(x)在R上是增函数
(2)若f+f(3x-9x-2)<0对?x∈R恒成立,求实数k的取值范围.
【答案】
分析:(1)任取x
1,x
2,且x
1<x
2,由f(x
2)-f(x
1)=f(x
2-x
1)及x>0时恒有f(x)>0可得f(x
2)与f(x
1)的大小关系,由函数单调性即可证明;
(2)f(k•3
x)+f(3
x-9
x-2)<0⇒f[(k•3
x)+(3
x-9
x-2)]<f(0),利用函数单调性可化为(k+1)•3
x-9
x-2<0恒成立,分离出参数k后转化为求函数最值即可.
解答:解:(1)任取x
1,x
2,且x
1<x
2,
由f(m+n)=f(m)+f(n),得f(m+n)-f(n)=f(m),
所以f(x
2)-f(x
1)=f(x
2-x
1),
又x>0时恒有f(x)>0,且x
2-x
1>0,
所以f(x
2-x
1)>0,即f(x
2)-f(x
1)>0,所以f(x
2)>f(x
1),
故f(x)在R上为增函数;
(2)令m=n=0,则由f(m+n)=f(m)+f(n),得f(0)=f(0)+f(0),所以f(0)=0,
f(k•3
x)+f(3
x-9
x-2)<0⇒f[(k•3
x)+(3
x-9
x-2)]<f(0),
由(1)知f(x)为增函数,所以(k•3
x)+(3
x-9
x-2)<0,即(k+1)•3
x-9
x-2<0,也即(k+1)<

,
所以f(k•3
x)+f(3
x-9
x-2)<0对?x∈R恒成立,等价于(k+1)<
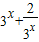
恒成立,
又
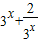
≥2

=2

,当且仅当

,即x=

时取得等号,
所以k+1<2

,即k<2

-1,
故实数k的取值范围为:k<2
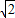
-1.
点评:本题考查函数恒成立问题,考查抽象函数单调性的判断,考查学生对问题的转化能力,恒成立问题经常转化为函数最值问题解决.

 ,
,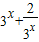 恒成立,
恒成立,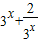 ≥2
≥2 =2
=2 ,当且仅当
,当且仅当 ,即x=
,即x= 时取得等号,
时取得等号, ,即k<2
,即k<2 -1,
-1,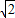 -1.
-1.
