Question

直线

3

x+y-2

3

=0截圆x²+y²=4得的劣弧所对的圆心角为（　　）

A．30°

B．45°

C．60°

D．90°

Answer 1

分析：由圆的标准方程找出圆心坐标和半径r，利用点到直线的距离公式求出圆心C到已知直线的距离d，由垂径定理及勾股定理求出直线被圆截得的弦长，由弦长等于圆的半径得到三角形ABC为等边三角形，即可得到直线被圆截得的劣弧所对的圆心角为60°．

解答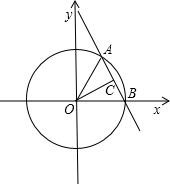：解：过O作OC⊥AB，垂足为点C，
由圆的方程x²+y²=4，得到圆心O的坐标为（0，0），半径r=2，
∵圆心到直线

3

x+y-2

3

=0的距离d=|OC|=

2 3

2

=

3

，
∴直线被圆截得的弦|AB|=2

r2-d2

=2，
∴△AOB为等边三角形，即∠AOB=60°，
∴直线被圆截的劣弧

AB

所对的圆心角为60°．
故选C

点评：此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，点到直线的距离公式，垂径定理，勾股定理，以及等边三角形的判定与性质，当直线与圆相交时，常常根据垂径定理由垂直得中点，再由弦长的一半，圆的半径及弦心距构造直角三角形，利用勾股定理来解决问题．