
【题目】给出下面类比推理:
①“若2a<2b,则a<b”类比推出“若a2<b2,则a<b”;
②“(a+b)c=ac+bc(c≠0)”类比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,则a=b”类比推出“a,b∈C,若a-b=0,则a=b”;
④“a,b∈R,若a-b>0,则a>b”类比推出“a,b∈C,若a-b>0,则a>b(C为复数集)”.
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图:
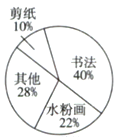

A学校 B学校
(1)从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解校园安全教育系列活动的成效,对全市高中生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化,现随机抽取部分高中生的答卷,统计结果如下,对应的频率分布直方图如图所示.
等级 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100) |
频数 | 12 |
| 48 | 24 |
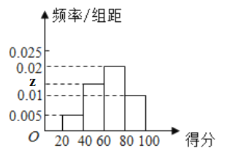
(1)求![]() 、
、![]() 的值;
的值;
(2)估计该市高中生测试成绩评定等级为“合格”的概率;
(3)在抽取的答卷中,用分层抽样的方法,从评定等级为“合格”和“不合格”的答卷中抽取5份,再从这5份答卷中任取2份,求恰有1份评定等级为“不合格”的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人某次飞镖游戏中的成绩如下:甲:8,6,7,7,8,10,9,8,7,8; 乙:9,10,6,7,9,9,10,8,9,10.其中甲的成绩可用如图(1)所示的打点图(或点状图)表示,每个成绩上面的点的个数表示这个成绩出现的次数.在图(2)中作出乙的成绩的打点图,并由图写出关于甲、乙成绩比较的两个统计结论.

![]()
(1) (2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入12月以业,在华北地区连续出现两次重污染天气的严峻形势下,我省坚持保民生,保蓝天,各地严格落实机动车限行等一系列“管控令”,某市交通管理部门为了了解市民对“单双号限行”的态度,随机采访了200名市民,将他们的意见和是否拥有私家车的情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断能否在犯错误的概率不超过![]() 的前提下认为“对限行的态度与是否拥有私家车有关”;
的前提下认为“对限行的态度与是否拥有私家车有关”;
(2)为了了解限行之后是否对交通拥堵、环境染污起到改善作用,从上述调查的不赞同限行的人员中按是否拥有私家车分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人没有私家车的概率.
附: 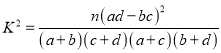 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把5件不同产品摆成一排.
(1)若产品A必须摆在正中间,排法有多少种?
(2)若产品A必须摆在两端,产品B不能摆在两端的排法有多少种?
(3)若产品A与产品B相邻,且产品A与产品C不相邻,则不同的排法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com