
【题目】函数y=x+sin|x|,x∈[﹣π,π]的大致图象是( )
A.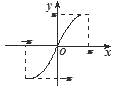
B.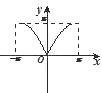
C.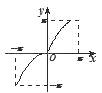
D.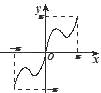
【答案】C
【解析】解答:由题意可知: ![]() , 当0≤x≤π时,∵y=x+sinx , ∴y′=1+cosx≥0,又y=cosx在[0,π]上为减函数,所以函数y=x+sinx在[0,π]上为增函数且增速越来越小;
, 当0≤x≤π时,∵y=x+sinx , ∴y′=1+cosx≥0,又y=cosx在[0,π]上为减函数,所以函数y=x+sinx在[0,π]上为增函数且增速越来越小;
当﹣π≤x<0时,∵y=x﹣sinx , ∴y′=1﹣cosx≥0,又y=cosx在[﹣π,0)上为增函数,所以函数y=x﹣sinx在[0,π]上为增函数且增速越来越小;
又函数y=x+sin|x|,x∈[﹣π,π],恒过(﹣π,﹣π)和(π,π)两点,所以C选项对应的图象符合.
故选C.
分析:本题考查的是函数的图象问题.在解答时,首先应将函数去绝对值转化为分段函数.再利用导数分析在不同区间段上的变化规律即可获得问题的解答.


科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为正数的等差数列,a1a2=3,a2a3=15.
(1)求数列{an}的通项公式;
(2)设bn=(an+1)2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
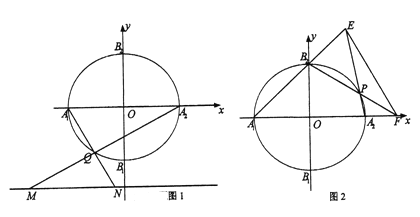
【题目】已知圆![]() 与坐标轴交于
与坐标轴交于![]() (如图).
(如图).
(1)点![]() 是圆
是圆![]() 上除
上除![]() 外的任意点(如图1),
外的任意点(如图1),![]() 与直线
与直线![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的最小值;
的最小值;
(2)点![]() 是圆
是圆![]() 上除
上除![]() 外的任意点(如图2),直线
外的任意点(如图2),直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() 的斜率为
的斜率为![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为 . 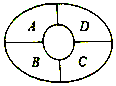
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为﹣3.
(1)求f(x)的解析式;
(2)求过点A(2,2)的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对函数中,相同的是( )
A.f(x)=lgx2 , g(x)=2lgx
B.f(x)=lg ![]() ,g(x)=lg(x+1)﹣lg(x﹣1)
,g(x)=lg(x+1)﹣lg(x﹣1)
C.f(u)= ![]() ,g(v)=
,g(v)= ![]()
D.f(x)=x,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用两角和与差的正弦、余弦公式证明:
sinαcosβ=![]() [sin(α+β)+sin(α﹣β)];
[sin(α+β)+sin(α﹣β)];
cosαsinβ=![]() [sin(α+β)﹣sin(α﹣β)];
[sin(α+β)﹣sin(α﹣β)];
cosαsinβ=![]() [cos(α+β)+cos(α﹣β)];
[cos(α+β)+cos(α﹣β)];
sinαcosβ=![]() [cos(α+β)﹣cos(α﹣β)].
[cos(α+β)﹣cos(α﹣β)].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com