Question

【题目】国内某知名大学有男生14000人，女生10000人，该校体育学院想了解本校学生的运动状况，根据性别采取分层抽样的方法从全校学生中抽取120人，统计他们平均每天运动的时间，如下表：（平均每天运动的时间单位：小时，该校学生平均每天运动的时间范围是）.

男生平均每天运动时间分布情况：

女生平均每天运动时间分布情况：

（1）请根据样本估算该校男生平均每天运动的时间（结果精确到0.1）；

（2）若规定平均每天运动的时间不少于2小时的学生为“运动达人”，低于2小时的学生为“非运动达人”.

①请根据样本估算该校“运动达人”的数量；

②请根据上述表格中的统计数据填写下面列联表，并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘运动达人’与性别有关？”

参考公式：，其中.

参考数据：

	0．10	0.05	0.025	0.010	0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1）1.5；（2）①4000；②在犯错误的概率不超过0.05的前提下不能认为“是否为‘运动达人’与性别有关”．

【解析】试题分析：（1）由分层抽样计算得男生抽人，女生抽人，故，由此求得男生平均运动事件为小时；（2）计算，故在犯错误的概率不超过的前提下不能认为“是否为‘运动达人’与性别有关”.

试题解析：

（1）由分层抽样得：男生抽取的人数为人，女生抽取人数为人，

故，

则该校男生平均每天运动时间为：

故该校男生平均每天运动的时间约为1.5小时；

（2）①样本中“运动达人”所占比例是，故估计该校“运动达人”有人；

②由表可知：

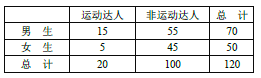
故的观测值

故在犯错误的概率不超过0.05的前提下不能认为“是否为‘运动达人’与性别有关”