
【题目】已知函数![]() .
.
(1)曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,求该切线方程;
,求该切线方程;
(2)若函数![]() 在区间
在区间![]() 上恒成立,且存在
上恒成立,且存在![]() 使得
使得![]() ,求
,求![]() 的值.
的值.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】缴纳个人所得税是收入达到缴纳标准的公民应尽的义务.
①个人所得税率是个人所得税额与应纳税收入额之间的比例;
②应纳税收入额=月度收入-起征点金额-专项扣除金额(三险一金等);
③2018年8月31日,第十三届全国人民代表大会常务委员会第五次会议《关于修改中华人民共和国个人所得税法的决定》,将个税免征额(起征点金额)由3500元提高到5000元.下面两张表格分别是2012年和2018年的个人所得税税率表:
2012年1月1日实行:
级数 | 应纳税收入额(含税) | 税率( | 速算扣除数 |
一 | 不超过1500元的部分 | 3 | 0 |
二 | 超过1500元至4500元的部分 | 10 | 105 |
三 | 超过4500元至9000元的部分 | 20 | 555 |
四 | 超过9000元至35000元的部分 | 25 | 1005 |
五 | 超过35000元至55000元的部分 | 30 | 2755 |
六 | 超过55000元至80000元的部分 | 35 | 5505 |
七 | 超过80000元的部分 | 45 | 13505 |
2018年10月1日试行:
级数 | 应纳税收入额(含税) | 税率( | 速算扣除数 |
一 | 不超过3000元的部分 | 3 | 0 |
二 | 超过3000元至12000元的部分 | 10 | 210 |
三 | 超过12000元至25000元的部分 | 20 | 1410 |
四 | 超过25000元至35000元的部分 | 25 | 2660 |
五 | 超过35000元至55000元的部分 | 30 | 4410 |
六 | 超过55000元至80000元的部分 | 35 | 7160 |
七 | 超过80000元的部分 | 45 | 15160 |
(1)何老师每月工资收入均为13404元,专项扣除金额3710元,请问何老师10月份应缴纳多少元个人所得税?若与9月份相比,何老师增加收入多少元?
(2)对于财务人员来说,他们计算个人所得税的方法如下:应纳个人所得税税额=应纳税收入额×适用税率-速算扣除数,请解释这种计算方法的依据?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 与直线
与直线![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.

(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,点M是PQ的中点,直线
两点,点M是PQ的中点,直线![]() 与直线
与直线![]() 相交于点N.探索
相交于点N.探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 与
与![]() 轴交于点
轴交于点![]() .(1)求证:
.(1)求证:![]() ,
,![]() ,
,![]() 成等比数列;
成等比数列;
(2)设![]() ,
,![]() ,试问
,试问![]() 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图半圆![]() 的直径为4,
的直径为4,![]() 为直径
为直径![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 为半圆周上任一点,以
为半圆周上任一点,以![]() 为边作等边
为边作等边![]() (
(![]() 、
、![]() 、
、![]() 按顺时针方向排列)
按顺时针方向排列)
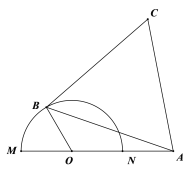
(1)若等边![]() 边长为
边长为![]() ,
,![]() ,试写出
,试写出![]() 关于
关于![]() 的函数关系;
的函数关系;
(2)问![]() 为多少时,四边形
为多少时,四边形![]() 的面积最大?这个最大面积为多少?
的面积最大?这个最大面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com