
【题目】已知正四棱柱的底面边长为![]() ,高为
,高为![]() ,现从该正四棱柱的
,现从该正四棱柱的![]() 个顶点中任取
个顶点中任取![]() 个点.设随机变量
个点.设随机变量![]() 的值为以取出的
的值为以取出的![]() 个点为顶点的三角形的面积.
个点为顶点的三角形的面积.
(1)求概率![]() ;
;
(2)求![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]()
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为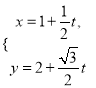 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-1|+|2x-1|.
(Ⅰ)若对![]() x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
(Ⅱ)在(Ⅰ)成立的条件下,正实数a,b满足a2+b2=2M.证明:a+b≥2ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
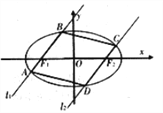
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
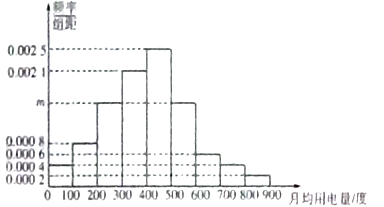
(Ⅰ)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2cos
=(2cos![]() ,
, ![]() sin
sin![]() ),
),![]() =(cos
=(cos![]() ,2cos
,2cos![]() ),(ω>0),设函数f(x)=
),(ω>0),设函数f(x)=![]()
![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求函数f(x)的表达式;
(2)求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com