
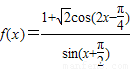 .若角
.若角 .
.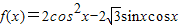 的图象按向量
的图象按向量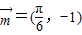 平移后,得到一个函数g(x)的图象,求g(x)的解析式.
平移后,得到一个函数g(x)的图象,求g(x)的解析式.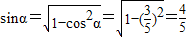 .…(2分)
.…(2分)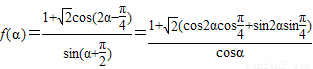 …(6分)
…(6分)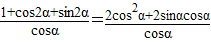 …(9分)
…(9分)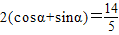 .…(10分)
.…(10分)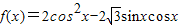 =cos2x-
=cos2x-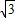 sin2x+1=2cos(2x+
sin2x+1=2cos(2x+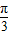 )+1;
)+1;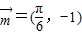 平移后,得到一个函数g(x)=2cos[2(x-
平移后,得到一个函数g(x)=2cos[2(x-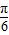 )+
)+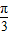 ]-1+1=2cos2x的图象,
]-1+1=2cos2x的图象,

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
1+
| ||||
sin(x+
|
| 3 |
| 5 |
| 3 |
| m |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高三第一次月考理科数学试卷(解析版) 题型:解答题
(本小题14分)
已知函数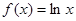 ,若
,若
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在区间
在区间 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;
(3)当
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省盐城市滨海中学高三(上)期中数学试卷(文科)(解析版) 题型:填空题
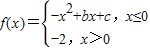 ,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .
,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com