如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B点在AM上，D点在AN上，且对角线MN过C点，已知|AB|=3米，|AD|=2米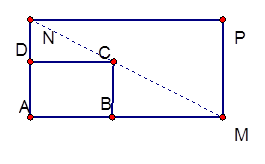
（1）要使矩形AMPN的面积大于32平方米，则AN的长度应在什么范围内？
（2）当AN的长度是多少时，矩形AMPN的面积最小？并求出最小值
科目：高中数学 来源： 题型：解答题
已知函数f(x)=|x-2|+2|x-a|(a∈R).
(I)当a=1时，解不等式f(x)>3;
(II)不等式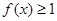
在区间（-∞，+∞)上恒成立，求实数a的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
∪
；（2）当AN的长度是4米时，矩形AMPN的面积最小，最小值为24平方米；
的取值范围，然后解对应的一元二次不等式；（2）利用分式拆分，构造基本不等式求最值；
， 由
，得
， 2分
4分
，得
，
，于是
，解得
，
12分
即
时，
取得最小值24，
.
的解集为
，求
的值；
，使
，求
满足
，
，试确定
的最大值.
的解集；
的解集非空，求实数
的取值范围.
.
的解集；
的不等式
在
上恒成立，求实数
的取值范围.
满足条件：
； ②
．
时，求
，
的值；
时，求证：
；
,且
，求证：
．
.
；
的解集为
，求实数
的取值范围.
的解集为
．
；
．