
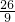 ,则OD+OE的最大值是________.
,则OD+OE的最大值是________.
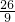 ,配方整理得3ab=2(a+b)2-(a+b)-
,配方整理得3ab=2(a+b)2-(a+b)- ,结合基本不等式建立不等关系,得2(a+b)2-(a+b)-
,结合基本不等式建立不等关系,得2(a+b)2-(a+b)- ≤
≤ (a+b)2,最后以a+b为单位解一元二次不等式,即可得到OD+OE的最大值.
(a+b)2,最后以a+b为单位解一元二次不等式,即可得到OD+OE的最大值.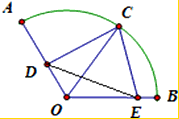
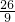
 =0,
=0, =0,即3ab=2(a+b)2-(a+b)-
=0,即3ab=2(a+b)2-(a+b)- …(*)
…(*) (a+b)]2=
(a+b)]2= (a+b)2,
(a+b)2, (a+b)2,代入(*)式,得2(a+b)2-(a+b)-
(a+b)2,代入(*)式,得2(a+b)2-(a+b)- ≤
≤ (a+b)2,
(a+b)2, ≤
≤ m2,
m2, m2-m-
m2-m- ≤0,得到-
≤0,得到- ≤m≤
≤m≤ ,
, ,即OD+OE的最大值是
,即OD+OE的最大值是 .
.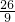 时,求OD+OE的最大值.着重考查了余弦定理、用基本不等式求最值和一元二次不等式的解法等知识,属于中档题.
时,求OD+OE的最大值.着重考查了余弦定理、用基本不等式求最值和一元二次不等式的解法等知识,属于中档题. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 26 |
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三第二学期第一次统考理科数学 题型:填空题
已知圆心角为120° 的扇形AOB半径为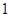 ,C为
,C为 中点.点D,E分别在半径OA,OB上.若CD 2+CE
2+DE 2=
中点.点D,E分别在半径OA,OB上.若CD 2+CE
2+DE 2=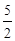 ,则OD+OE的取值范围是 .
,则OD+OE的取值范围是 .

查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三第二学期第一次统考文科数学 题型:填空题
已知圆心角为120° 的扇形AOB半径为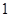 ,C为
,C为 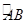 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是 .
中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是 .

查看答案和解析>>
科目:高中数学 来源:2012届浙江省高三调研测试理科数学试卷 题型:填空题
已知圆心角为120° 的扇形AOB半径为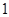 ,C为
,C为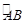 中点.点D,E分别在半径OA,OB上.若CD 2+CE 2+DE 2=
中点.点D,E分别在半径OA,OB上.若CD 2+CE 2+DE 2=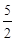 ,则OD+OE的取值范围是 .
,则OD+OE的取值范围是 .

查看答案和解析>>
科目:高中数学 来源:2012届浙江省高三调研测试文科数学试卷 题型:填空题
已知圆心角为120° 的扇形AOB半径为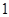 ,C为
,C为 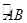 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是 .
中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=2,则OD+OE的最大值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com