
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
科目:高中数学 来源: 题型:
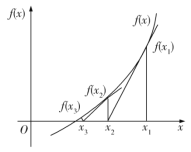
【题目】牛顿迭代法(Newton's method)又称牛顿–拉夫逊方法(Newton–Raphsonmethod),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设![]() 是
是![]() 的根,选取
的根,选取![]() 作为
作为![]() 初始近似值,过点
初始近似值,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 与
与![]() 轴的交点的横坐标
轴的交点的横坐标![]() ,称
,称![]() 是
是![]() 的一次近似值,过点
的一次近似值,过点![]() 作曲线
作曲线![]() 的切线,则该切线与
的切线,则该切线与![]() 轴的交点的横坐标为
轴的交点的横坐标为![]() ,称
,称![]() 是
是![]() 的二次近似值.重复以上过程,直到
的二次近似值.重复以上过程,直到![]() 的近似值足够小,即把
的近似值足够小,即把![]() 作为
作为![]() 的近似解.设
的近似解.设![]() 构成数列
构成数列![]() .对于下列结论:
.对于下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100位学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.
(1)请先求出频率分布表中①②位置相应的数据,再在答题纸上完成下列频率分布直方图(如图所示);
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| ① | 0.350 |
第3组 |
| 30 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
频率分布直方图
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6位学生进入第二轮面试,求第3、4、5组每组各抽取多少位学生进入第二轮面试;
(3)在(2)的前提下,学校决定在6位学生中随机抽取2位学生接受A考官进行面试,求第4组至少有一位学生被考官A面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某产品1到6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与单价仍然服从(1)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y,z为空间不同的直线或不同的平面,且直线不在平面内,下列说法能保证“若![]() ,
,![]() ,则
,则![]() ”为真命题的序号为______.
”为真命题的序号为______.
①x为直线,y,z为平面;
②x,y,z都为平面;
③x,y为直线,z为平面;
④x,y,z都为直线;
⑤x,y为平面,z为直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]()
(1)若“![]() x∈A,使得x∈B”为真命题,求m的取值范围;
x∈A,使得x∈B”为真命题,求m的取值范围;
(2)是否存在实数m,使“x∈A”是“X∈B”必要不充分条件,若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与双曲线
与双曲线![]() 有公共焦点
有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)以双曲线![]() 的另一焦点
的另一焦点![]() 为圆心的圆
为圆心的圆![]() 与直线
与直线![]() 相切,圆
相切,圆![]() .过点
.过点![]() 作互相垂直且分别与圆
作互相垂直且分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,问:
,问:![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=![]() (a≠0).
(a≠0).
(1)当a=-1,b=0时,求函数f (x)的极值;
(2)当b=1时,若函数f (x)没有零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)统计某校![]() 名学生的某次数学同步练习成绩(满分150分),根据成绩依次分成六组:
名学生的某次数学同步练习成绩(满分150分),根据成绩依次分成六组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到频率分布直方图如图所示,若不低于140分的人数为110,则下列说法正确的是( )
,得到频率分布直方图如图所示,若不低于140分的人数为110,则下列说法正确的是( )
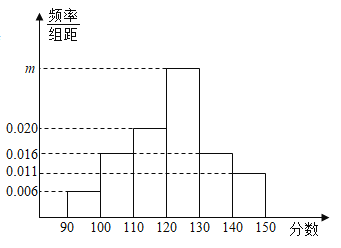
A.![]() B.
B.![]()
C.100分以下的人数为60D.成绩在区间![]() 内的人数占大半
内的人数占大半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com