Question

三棱锥P-ABC的高为PH，若三个侧面两两垂直，则H为△ABC的

1. A.
   内心
2. B.
   外心
3. C.
   垂心
4. D.
   重心

Answer 1

C
分析：先画出图形，三个侧面两两垂直，可看成正方体的一角，根据BC⊥面APH，而AH?面APH，推出AH⊥BC，同理可推出CH⊥AB，得到H为△ABC的垂心．
解答：如图所示，

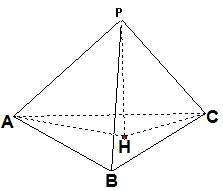
三个侧面两两垂直，可看成正方体的一角，则AP⊥面PBC，
而BC?平面PBC∴AP⊥BC而PH⊥面ABC，BC?面ABC
∴PH⊥BC，又AP∩PH=P，
∴BC⊥面APH，而AH?面APH
∴AH⊥BC，同理可得CH⊥AB
故H为△ABC的垂心
故选：C
点评：本题主要考查了平面与平面垂直的性质，以及棱锥的结构特征，考查空间想象能力、运算能力和推理论证能力，属于基础题．