
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时,
(单位:瓶)为多少时,![]() 的数学期望达到最大值?
的数学期望达到最大值?
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 两个变量的相关关系一定是线性相关
B. 两个随机变量的线性相关线越强,则相关系数的绝对值就越接近于0
C. 在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加1个单位
平均增加1个单位
D. 对分类变量![]() 与
与![]() ,随机变量
,随机变量![]() 的观测值
的观测值![]() 越大,则判断“
越大,则判断“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过![]() 的有20人,不超过
的有20人,不超过![]() 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过的人与性别有关;
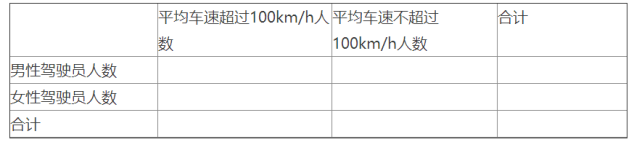
(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过![]() 的车辆数为
的车辆数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的数学期望.
的数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
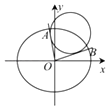
【题目】如图所示,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为
=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(x0 , y0)是椭圆C上的动点,过原点O引两条射线l1 , l2与圆M:(x﹣x0)2+(y﹣y0)2= ![]() 分别相切,且l1 , l2的斜率k1 , k2存在.
分别相切,且l1 , l2的斜率k1 , k2存在.
①试问k1k2是否定值?若是,求出该定值,若不是,说明理由;
②若射线l1 , l2与椭圆C分别交于点A,B,求|OA||OB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量M之间的关系为:![]() ,(其中a,b是实数),据统计,该种鸟类在静止的时间其耗氧量为45个单位,而其耗氧量为105个单位时,其飞行速度为1m/s.
,(其中a,b是实数),据统计,该种鸟类在静止的时间其耗氧量为45个单位,而其耗氧量为105个单位时,其飞行速度为1m/s.
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要多少个单位。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC= ![]() .
. 
(1)求证:B1C1∥平面BCD1;
(2)求证:平面A1ABB1⊥平面BCD1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com