[题目]设为三角形的三边.求证: 题目和参考答案——青夏教育精英家教网—

【题目】设为三角形的三边，求证：

【答案】见解析

【解析】试题分析：本题用直接法不易找到证明思路，用分析法，要证该不等式成立，因为，所以，只需证该不等式两边同乘以转化成的等价不等式a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)成立，用不等式性质整理为a+2ab+b+abc>c成立，用不等式性质及三角不等式很容易证明此不等式成立.

试题解析：要证明：

需证明： a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b) 5分

需证明:a(1+b+c+bc)+ b(1+a+c+ac)> c(1+a+b+ab) 需证明a+2ab+b+abc>c 10分

∵a,b,c是的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0

∴a+2ab+b+abc>c

∴成立。 14分

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】甲、乙两人为了响应政府“节能减排”的号召，决定各购置一辆纯电动汽车．经了解目前市场上销售的主流纯电动汽车，按续驶里程数（单位：公里）可分为三类车型，，．甲从三类车型中挑选，乙从两类车型中挑选，甲、乙两人选择各类车型的概率如表：

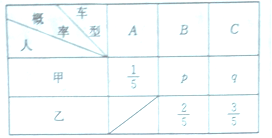
已知甲、乙都选类型的概率为.

（1）求的值；

（2）求甲、乙选择不同车型的概率；

（3）某市对购买纯电动汽车进行补贴，补贴标准如下表：

记甲、乙两人购车所获得的财政补贴之和为，求的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某届奥运会上，中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二，某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查（结果只有“满意”和“不满意”两种），从被调查的学生中随机抽取了50人，具体的调查结果如下表：

(1)在高三年级全体学生中随机抽取一名学生，由以上统计数据估计该生持满意态度的概率；

(2)若从一班至二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为，求随机变量的分布列及数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】张师傅想要一个如图1所示的钢筋支架的组合体，来到一家钢制品加工店定制，拿出自己画的组合体三视图（如图2所示）.店老板看了三视图，报了最低价，张师傅觉得很便宜，当即甩下定金和三视图，约定第二天提货.第二天提货时，店老板一脸坏笑的捧出如图3–1所示的组合体，张师傅一看，脸都绿了：“奸商，怎能如此偷工减料”.店老板说，我是按你的三视图做的，要不我给你加一个正方体，但要加价，随机加上了一个正方体，得到如图3–2所示的组合体；张师傅脸还是绿的，店老板又加上一个正方体，组成了如图 3–3 所示的组合体，又加价；张师傅脸继续绿，店老板再加一个正方体，组成如图 3–4 所示的组合体，再次加价；双方就三视图争吵不休……

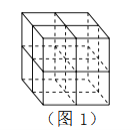
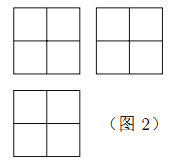
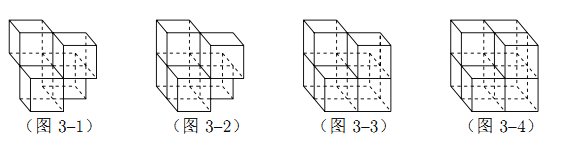
你认为店老板提供的个组合体的三视图与张师傅画的三视图一致的个数是（）

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知某商品的进货单价为1元/件，商户甲往年以单价2元/件销售该商品时，年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算，若今年的实际销售单价为元/件（），则新增的年销量（万件）.

（1）写出今年商户甲的收益（单位：万元）与的函数关系式；

（2）商户甲今年采取降低单价提高销量的营销策略，是否能获得比往年更大的收益（即比往年收益更多）？请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某单位实行休年假制度三年以来，50名职工休年假的次数进行的调查统计结果如下表所示：

休假次数	0	1	2	3
人数	5	10	20	15

根据表中信息解答以下问题：

（1）从该单位任选两名职工，求这两人休年假次数之和为4的概率；

（2）从该单位任选两名职工，用表示这两人休年假次数之差的绝对值，求随机变量的分布列及数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数（单位：μg/m3）为0~50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50~100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100~150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150~200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200~300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．2017年1月某日某省x个监测点数据统计如下：

空气污染指数

（单位：μg/m3）