
【题目】四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求二面角D﹣AE﹣C的大小.
,求二面角D﹣AE﹣C的大小.
【答案】
(1)证明:连结BD交AC于点O,连结EO,
∵ABCD为矩形,∴O为BD的中点,
又E为的PD的中点,∴EO∥PB,
EO平面AEC,PB平面AEC,
∴PB∥平面AEC
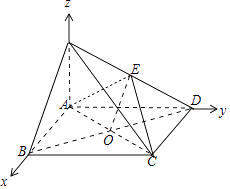
(2)解:∵PA⊥平面ABCD,ABCD为矩形,
∴AB,AD,AP两两垂直,
如图,以A为坐标原点, ![]() 的方向为x轴的正方向,
的方向为x轴的正方向,
建立空间直角坐标系A﹣xyz,
∵AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,
,
∴三棱锥P﹣ABD的体积 ![]() ,得
,得 ![]() .
.
则A(0,0,0),D(0, ![]() ,0),B(
,0),B( ![]() ,0,0),E(0,
,0,0),E(0, ![]() ,
, ![]() ),C (
),C ( ![]() ,
, ![]() ,0),
,0),
则 ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,0)
,0)
设 ![]() 为平面ACE的法向量,
为平面ACE的法向量,
则 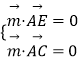 ,即
,即 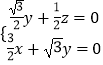 ,令x=1,得
,令x=1,得 ![]() ,
, ![]() ,则
,则 ![]() =(1,
=(1, ![]() ,
, ![]() ),
),
又 ![]() 为平面DAE的法向量,
为平面DAE的法向量,
∴cos< ![]() >=
>= 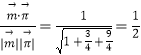 ,
,
如图可得二面角D﹣AE﹣C为锐角,∴二面角D﹣AE﹣C为 ![]() .
.
【解析】(1)连结BD交AC于点O,连结EO,由已知可得EO∥PB,然后利用线面平行的判定可得PB∥平面AEC;(2)由PA⊥平面ABCD,ABCD为矩形,可得AB,AD,AP两两垂直,以A为坐标原点, ![]() 的方向为x轴的正方向,建立空间直角坐标系A﹣xyz,再由三棱锥P﹣ABD的体积V=
的方向为x轴的正方向,建立空间直角坐标系A﹣xyz,再由三棱锥P﹣ABD的体积V= ![]() 求得AB,得到A,D,B,E,C的坐标,然后求出平面ACE与平面DAE的法向量,由两法向量所成角的余弦值求得二面角D﹣AE﹣C的大小.
求得AB,得到A,D,B,E,C的坐标,然后求出平面ACE与平面DAE的法向量,由两法向量所成角的余弦值求得二面角D﹣AE﹣C的大小.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=2cos2x+ ![]() sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此时的x值
(2)求f(x)的单调减区间
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
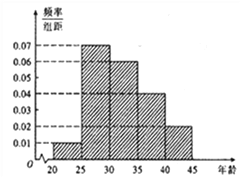
(1)分别求第3,4,5组的频率.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,我市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
(1)求椭圆的标准方程
(2)设直线l:y=kx+1与椭圆C相交于P,Q两点,是否存在这样的实数k,使得以PQ为直径的圆过原点,若存在,请求出k的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax﹣a﹣x(a>0且a≠1)
(1)若f(1)<0,求a的取值范围;
(2)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2mf(x)且g(x)在[1,+∞)上的最小值为﹣2,求m的值.
,g(x)=a2x+a﹣2x﹣2mf(x)且g(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】F1 , F2分别是双曲线x2﹣ ![]() =1(b>0)的左、右焦点,过F2的直线l与双曲线的左右两支分别交于A,B两点,若△ABF1是等边三角形,则该双曲线的虚轴长为( )
=1(b>0)的左、右焦点,过F2的直线l与双曲线的左右两支分别交于A,B两点,若△ABF1是等边三角形,则该双曲线的虚轴长为( )
A.2 ![]()
B.2 ![]()
C.![]()
D.4 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com