练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某人对一个地区人均工资x与该地区人均消费y进行统计调查得y与x具有相关关系，且回归直线方程为
    y
    =0.66x+1.562（单位：千元），若该地区人均消费水平为7.675，估计该地区人均消费额占人均工资收入的百分比约为______．（精确到0.1%）
    ∵y与x具有线性相关关系，满足回归方程y=0.66x+1.562，
    该地区人均消费水平为y=7.675，
    ∴可以估计地区的职工均工资水平7.675=0.66x+1.562，
    ∴x=9.262，
    ∴可以估计地区人均消费额占人均工资收入的百分比约为
    7.675
    9.262
    ×100%=82.9%，
    故答案为：82.9%．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

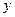    某种产品表面进行腐蚀性试验，得到腐蚀深度与腐蚀时间之间对应的一组数据：
    时间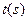
    		深度
    5
    		6
    10
    		10
    15
    		10
    20
    		13
    30
    		16
    40
    		17
    50
    		19
    60
    		23
    70
    		25
    90
    		29
    120
    		46
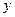    （1）试求腐蚀深度对时间的回归直线方程；
    （2）预测腐蚀时间为80 s时产品腐蚀的深度大约是多少？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    假设关于某种设备的使用年限和支出的维修费用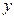（万元），有以下的统计资料：
    使用年限
    		2
    		3
    		4
    		5
    		6
    维修费用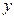
    		2.2
    		3.8
    		5.5
    		6.5
    		7.0
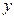     （1）求支出的维修费用与使用年限的线性回归方程；
    （2）估计使用年限为10年时，维修费用是多少？
    （）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    相关关系与函数关系的区别是                             ．          

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某超市在一段时间内的某种商品的价格x（元）与销售量y（kg）之间的一组数据如下表所示：
    价格x（元）11.411.611.812.012.2
    销售量y（kg）112110107105103
    （Ⅰ）画出散点图；
    （Ⅱ）求出y对x的回归的直线方程；
    （Ⅲ）当价格定为11.9元时，预测销售量大约是多少？
    b
    =
    n
    i=1
    (x1-
    .
    x
    )(y1-
    .
    y
    )
    n
    i=1
    (x1-
    .
    x
    )    2
    =
    n
    i=1
    x1y1-n
    .
    x
    .
    y
    n
    i=1
    x    		21
    -n
    .
    x
    2
    ．

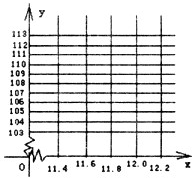
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设有一个回归方程
    y
    =3-2.5x    ，则变量x增加一个单位时（　　）
    A．y平均增加2.5个单位B．y平均增加3个单位
    C．y平均减少2.5个单位D．y平均减少3个单位

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知两个变量x与y之间具有线性相关关系，5次试验的观测数据如下：
    x100120140160180
    y4554627592
    那么变量y关于x的回归直线方程只可能是（　　）
    A．
    y
    =0.575x-14.9    		B．
    y
    =0.572x-13.9
    C．
    y
    =0.575x-12.9    		D．
    y
    =0.572x-14.9

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    两个变量有线性相关关系且正相关，则回归直线方程中，
    y
    =bx+a    的系数b（　　）
    A．b＞0B．b＜0C．b=0D．b=1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    数据x1,x2, …,x8的平均数为6，标准差为2，则数据2x1-6,2x2-6, …,2x8-6的平均数为___________，方差为_________.

    查看答案和解析>>

    同步练习册答案