
【题目】已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若m∥n,n⊥β,mα,则α⊥β;
②若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;
③若m⊥α,m⊥n,nβ,则α∥β或α⊥β;
④若α∩β=m,n∥m,nα,nβ,则n∥α且n∥β;
其中正确命题的序号是( )
A.①②B.①③C.①④D.②④
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】某学校在学期结束,为了解家长对学校工作的满意度,对两个班的100位家长进行满意度调查,调查结果如下:
非常满意 | 满意 | 合计 | |
A | 30 | 15 | 45 |
B | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
(1)根据表格判断是否有![]() 的把握认为家长的满意程度与所在班级有关系?
的把握认为家长的满意程度与所在班级有关系?
(2)用分层抽样的方法从非常满意的家长中抽取5人进行问卷调查,并在这5人中随机选出2人进行座谈,求这2人都来自同一班级的概率?
附:
|
|
|
|
|
|
|
|
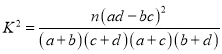
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,△DAB≌△DCB,E为线段BD上的点,且EA=EB=ED=AB,延长CE交AD于点F.
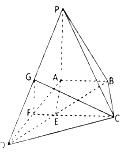
(1)若G为PD的中点,求证平面PAD⊥平面CGF;
(2)若AD=AP=6,求平面BCP与平面DCP所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某美术学院2018年在山西招生,报名人数很多.工作人员在某个市区抽取了该区2018年美术招生考试成绩中200名学生的色彩和素描的初试成绩,按成绩分组,得到的频率分布表如下图所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 24 | 0.12 |
第2组 |
| ① | 0.18 |
第3组 |
| 64 | 0.32 |
第4组 |
| 60 | ② |
第5组 |
| 16 | 0.08 |
合计 | 200 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图,并由频率分布直方图估算中位数;
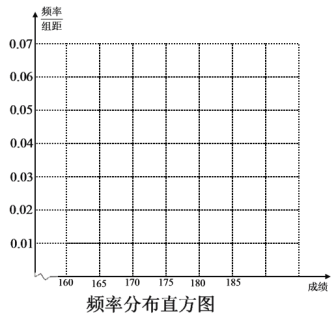
(2)为了能更清楚地了解该市学生的情况,该美院决定在复试以前先进行抽样调研.但受场地和教授人数的客观限制,决定从第3组选出3人,第4组选出2人,第5组选出1人,然后从这6人中再选出2人进行调研,求这2人均来自第三组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆E:![]() y2=1的左、右焦点,过点P(﹣2,0)的直线l与椭圆E有且只有一个交点T.
y2=1的左、右焦点,过点P(﹣2,0)的直线l与椭圆E有且只有一个交点T.
(1)求△F1TF2的面积;
(2)求证:光线![]() 被直线反射后经过F2.
被直线反射后经过F2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x﹣1|+|2x+1|<3的解集为{x|a<x<b};
(1)求a,b的值;
(2)若正实数x,y满足x+y=ab+2且不等式(yc2﹣4)x+(8cx﹣1)y≤0对任意的x,y恒成立,求实数c的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,且
,且![]() .点
.点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .
.
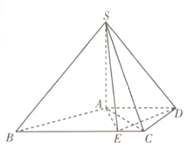
(1)求证:平面![]() 平面
平面![]() .
.
(2)若![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com